题目内容
【题目】我们定义：在平面直角坐标系
中，经过点
，且平行于直线
或
，叫过该点的“二维线”．例如，点
的“二维线”有：
，
．
（1）写出点
的“二维线”______；
（2）若点的“二维线”是
，
，求
、
的值；
（3）若反比例函数
图像上的一个点有一条“二维线”是
，求
点的另一条“二维线”．
【答案】（1）
，
；（2）
，
；（3）
或
．
【解析】
（1）根据“二维线”的定义和待定系数法解答即可；
（2）把点
分别代入两个一次函数关系式可得关于m、n的方程组，解方程组即得结果；
（3）把点分别代入反比例函数和一次函数关系式可得关于m、n的方程组，解方程组即可求出m、n的值，再根据“二维线”的定义即可求得结果．
解：（1）设点
的“二维线”是：
与
，
把点分别代入，得
，
，
解得：
，
，
∴点的“二维线”是：，；
故答案为：，；
（2）根据题意，得：
，解得：，；
（3）由题意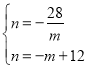，得：
，解得：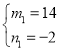
，
，
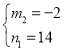设点的另一条“二维线”是
，
当m=14，n=﹣2时，﹣2=14+a，解得：a=﹣16；
当m=﹣2，n=14时，14=﹣2+a，解得：a=16；
∴点的另一条“二维线”是或．
【题目】意外创伤随时可能发生，急救是否及时、妥善，直接关系到病人的安危．为普及急救科普知识，提高学生的急救意识与现场急救能力，某校开展了急救知识进校园培训活动．为了解七、八年级学生(七、八年级各有600名学生)的培训效果，该校举行了相关的急救知识竞赛．现从两个年级各随机抽取20名学生的急救知识竞赛成绩(百．分制)进行分析，过程如下：
收集数据：
七年级：79，85，73，80，75，76，87，70，75，94，75，78，81，72，75，80，86，59，83，77．
八年级：92，74，87，82，72，81，94，83，77，83，80，81，71，81，72，77，82，80，70，41．
整理数据：
40≤x≤49 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 | |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据：
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 | c |
八年级 | 78 | d | 80.5 |
应用数据：
（1）由上表填空：a＝ ；b＝ ；c＝ ；d＝ ．
（2）估计该校七、八两个年级学生在本次竞赛中成绩在80分及以上的共有多少人？
（3）你认为哪个年级的学生对急救知识掌握的总体水平较好，请说明理由．
