题目内容
【题目】如图①,在边长为8的等边△ABC中,CD⊥AB,垂足为D,⊙O的圆心与点D重合,⊙O与线段CD交于点E,若将⊙O沿DC方向向上平移1cm后,如图②,⊙O恰与△ABC的边AC,BC相切,则图①中CE的长为cm. 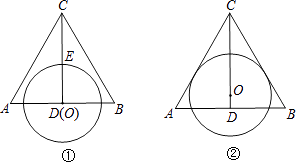
【答案】(2 ![]() ﹣
﹣ ![]() )
)
【解析】解: 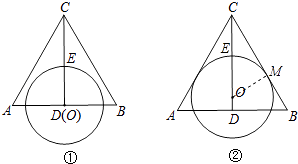
如图,设图②中圆O与BC的切点为M,
连接OM,
则OM⊥MC,
∴∠OMC=90°,
依题意知道∠DCB=30°,
设OM为rcm,
∵△ABC是等边三角形,AB=8
∴CD= ![]() ×8=4
×8=4 ![]() cm,
cm,
∵⊙O沿DC方向向上平移1cm,
∴OD=1cm,
∴sin∠DCB= ![]() =
= ![]() ,
,
∴CO=2r,
∴1+2r=4 ![]() ,
,
∴r= ![]() ,
,
∴CE=CD﹣OE﹣OD=4 ![]() ﹣
﹣ ![]() ﹣1=(2
﹣1=(2 ![]() ﹣
﹣ ![]() )cm,
)cm,
故答案为:2 ![]() ﹣
﹣ ![]() .
.
如图,设圆O与BC的切点为M,连接OM,根据切线的性质可以得到∠OMC=90°,而根据已知条件可以得到∠DCB=30°,设OM为rcm,根据CD=CO+OD列出方程即可解决问题.

练习册系列答案
相关题目