题目内容
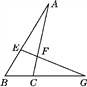
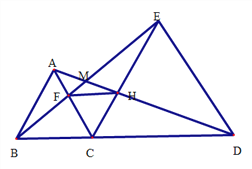
【题目】如图,已知△ABC和△ECD都是等边三角形, B、C、D在一条直线上。
求证:(1)BE=AD;
(2)CF=CH;
(3)△FCH是等边三角形;
(4)FH∥BD;
(5)求∠EMD的度数。;
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析;(4)证明见解析;(5)∠EMD
的度数为60°.
【解析】试题分析:(1)根据△ABC和△CDE都是等边三角形得出BC=AC,CE=CD,∠BCA=∠ECD=60°,再由SAS定理即可得出△BCE≌△ACD,进而得到BE=AD;(2)(3)利用△BCE≌△ACD得出∠CBF=∠CAH,再运用平角定义得出∠BCF=∠ACH进而得出△BCF≌△ACH因此CF=CH,再由∠ACH=60°根据“有一个角是60°的三角形是等边三角形可得△CFH是等边三角形.(4)由△FCH是等边三角形,∠FHC =∠HCD =60°,即可得到FH∥BD;(5)
由△BCE≌△ACD得∠BEC =∠ADC,∠MEH =∠CDH∠MHE =∠CHD可得∠EMH =∠HCD=60°.
试题解析:(1)∵△ABC和△DEC是等边三角形,
∴AC=BC.CE=CD,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,
∴∠BCE=∠ACD,
在△BCE和△ACD中,
AC=BC ∠BCE=∠ACD CE=CD
∴△BCE≌△ACD(SAS), ∴AD=BE.
(2)∵△BCE≌△ACD,
∴∠BCE=∠ADC.
∵∠FCE=∠HCD=60°
在△FCE和△HCD中,
∠BCE=∠ADC CE =CD ∠FCE=∠HCD
∴△BCE≌△ACD (ASA),
∴CF =CH
: 在△CFH中
∵ CF=CH ∠FCH=60°
∴△FCH是等边三角形
(4): ∵△FCH是等边三角形
∴∠FHC =60°
∵∠HCD =60° ∴∠FHC=∠HCD
∴FH∥BD
(5): ∵ △BCE≌△ACD
∴∠BEC =∠ADC
在△MHE和△CHD中
∵∠MEH =∠CDH
∠MHE =∠CHD(对顶角相等)
∴∠EMH =∠HCD=60°
∠EMD=60°

 优学名师名题系列答案
优学名师名题系列答案【题目】“中国梦”关乎每个人的幸福生活,为进一步感知我们身边的幸福,展现成都人追梦的风采,我市某校开展了以“梦想中国,逐梦成都”为主题的摄影大赛,要求参赛学生每人交一件作品.现将参赛的50件作品的成绩(单位:分)进行统计如下:
等级 | 成绩(用s表示) | 频数 | 频率 |
A | 90≤s≤100 | x | 0.08 |
B | 80≤s<90 | 35 | y |
C | s<80 | 11 | 0.22 |
合 计 | 50 | 1 |
请根据上表提供的信息,解答下列问题:
(1)表中的x的值为 , y的值为
(2)将本次参赛作品获得A等级的学生依次用A1 , A2 , A3 , …表示,现该校决定从本次参赛作品中获得A等级学生中,随机抽取两名学生谈谈他们的参赛体会,请用树状图或列表法求恰好抽到学生A1和A2的概率.