题目内容
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() 和实数
和实数![]() ,给出如下定义:当
,给出如下定义:当![]() 时,以点
时,以点![]() 为圆心,
为圆心,![]() 为半径的圆,称为点
为半径的圆,称为点![]() 的
的![]() 倍相关圆.
倍相关圆.
例如,在如图1中,点![]() 的1倍相关圆为以点
的1倍相关圆为以点![]() 为圆心,2为半径的圆.
为圆心,2为半径的圆.
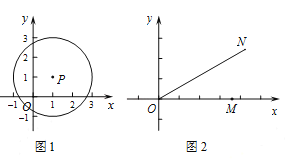
(1)在点![]() 中,存在1倍相关圆的点是________,该点的1倍相关圆半径为________.
中,存在1倍相关圆的点是________,该点的1倍相关圆半径为________.
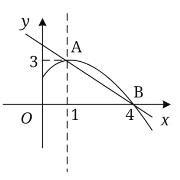
(2)如图2,若![]() 是
是![]() 轴正半轴上的动点,点
轴正半轴上的动点,点![]() 在第一象限内,且满足
在第一象限内,且满足![]() ,判断直线
,判断直线![]() 与点
与点![]() 的
的![]() 倍相关圆的位置关系,并证明.
倍相关圆的位置关系,并证明.
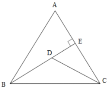
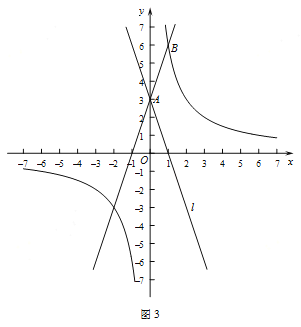
(3)如图3,已知点![]() ,反比例函数
,反比例函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称.
轴对称.
①若点![]() 在直线
在直线![]() 上,则点
上,则点![]() 的3倍相关圆的半径为________.
的3倍相关圆的半径为________.
②点![]() 在直线
在直线![]() 上,点
上,点![]() 的
的![]() 倍相关圆的半径为
倍相关圆的半径为![]() ,若点
,若点![]() 在运动过程中,以点
在运动过程中,以点![]() 为圆心,
为圆心,![]() 为半径的圆与反比例函数
为半径的圆与反比例函数![]() 的图象最多有两个公共点,直接写出
的图象最多有两个公共点,直接写出![]() 的最大值.
的最大值.
【答案】(1)解:![]() ,3(2)解:直线
,3(2)解:直线![]() 与点
与点![]() 的
的![]() 倍相关圆的位置关系是相切. (3)①点
倍相关圆的位置关系是相切. (3)①点![]() 的3倍相关圆的半径是3;②
的3倍相关圆的半径是3;②![]() 的最大值是
的最大值是![]() .
.
【解析】
(1)根据点![]() 的
的![]() 倍相关圆的定义即可判断出答案;
倍相关圆的定义即可判断出答案;
(2)设点![]() 的坐标为
的坐标为![]() ,求得点
,求得点![]() 的
的![]() 倍相关圆半径为
倍相关圆半径为![]() ,再比较与点
,再比较与点![]() 到直线直线
到直线直线![]() 的距离即可判断;
的距离即可判断;
(3)①先求得直线![]() 的解析式,
的解析式,
(1)![]() 的1倍相关圆,半径为:
的1倍相关圆,半径为:![]() ,
,
![]() 的1倍相关圆,半径为:
的1倍相关圆,半径为:![]() ,不符合,
,不符合,
故答案为:![]() ,3;
,3;
(2)解:直线![]() 与点
与点![]() 的
的![]() 倍相关圆的位置关系是相切,
倍相关圆的位置关系是相切,
证明:设点![]() 的坐标为
的坐标为![]() ,过
,过![]() 点作
点作![]() 于点
于点![]() ,
,
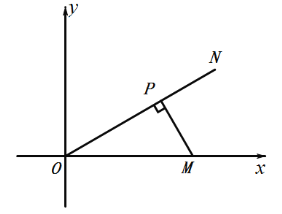
∴点![]() 的
的![]() 倍相关圆半径为
倍相关圆半径为![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴点![]() 的
的![]() 倍相关圆半径为
倍相关圆半径为![]() ,
,
∴直线![]() 与点
与点![]() 的
的![]() 倍相关圆相切,
倍相关圆相切,
(3)①∵反比例函数![]() 的图象经过点
的图象经过点![]() ,
,
∴![]() ,
,
∴点B的坐标为:![]() ,
,
∵直线![]() 经过点
经过点![]() 和
和![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入得:
代入得:![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
∵直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称,
轴对称,
∴直线![]() 的解析式为:
的解析式为:![]() ,
,
∵点![]() 在直线
在直线![]() 上,
上,
设点C的坐标为:![]() ,
,
∴点![]() 的3倍相关圆的半径是:
的3倍相关圆的半径是:![]() ,
,
故点![]() 的3倍相关圆的半径是3;
的3倍相关圆的半径是3;
②![]() 的最大值是
的最大值是![]() .
.

练习册系列答案
相关题目