题目内容
 如图,梯形ABCD中,AB∥CD,点E、F、G分别是BD、AC、DC的中点.已知两底差是8,两腰和是12,则△EFG的周长是
如图,梯形ABCD中,AB∥CD,点E、F、G分别是BD、AC、DC的中点.已知两底差是8,两腰和是12,则△EFG的周长是
- A.8
- B.9
- C.10
- D.12
C
分析:根据三角形中位线定理易得所求的三角形的各边长为原三角形各边长的一半,那么所求的三角形的周长就等于原三角形周长的一半.
解答: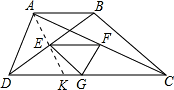 解:连接AE,并延长交CD于K,
解:连接AE,并延长交CD于K,
∵AB∥CD,
∴∠BAE=∠DKE,∠ABD=∠EDK,
∵点E、F、G分别是BD、AC、DC的中点.
∴BE=DE,
∴△AEB≌△KED,
∴DK=AB,AE=EK,EF为△ACK的中位线,
∴EF= CK=
CK= (DC-DK)=
(DC-DK)= (DC-AB),
(DC-AB),
∵EG为△BCD的中位线,∴EG= BC,
BC,
又FG为△ACD的中位线,∴FG= AD,
AD,
∴EG+GF= (AD+BC),
(AD+BC),
∵两腰和是12,即AD+BC=12,两底差是8,即DC-AB=8,
∴EG+GF=6,FE=4,
∴△EFG的周长是6+4=10.
故选C.
点评:此题考查的是三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半.
分析:根据三角形中位线定理易得所求的三角形的各边长为原三角形各边长的一半,那么所求的三角形的周长就等于原三角形周长的一半.
解答:
 解:连接AE,并延长交CD于K,
解:连接AE,并延长交CD于K,∵AB∥CD,
∴∠BAE=∠DKE,∠ABD=∠EDK,
∵点E、F、G分别是BD、AC、DC的中点.
∴BE=DE,
∴△AEB≌△KED,
∴DK=AB,AE=EK,EF为△ACK的中位线,
∴EF=
 CK=
CK= (DC-DK)=
(DC-DK)= (DC-AB),
(DC-AB),∵EG为△BCD的中位线,∴EG=
 BC,
BC,又FG为△ACD的中位线,∴FG=
 AD,
AD,∴EG+GF=
 (AD+BC),
(AD+BC),∵两腰和是12,即AD+BC=12,两底差是8,即DC-AB=8,
∴EG+GF=6,FE=4,
∴△EFG的周长是6+4=10.
故选C.
点评:此题考查的是三角形中位线的性质,即三角形的中位线平行于第三边且等于第三边的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
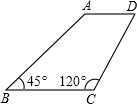 已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
已知,如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )A、
| ||||
B、4
| ||||
C、
| ||||
D、4
|
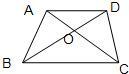 5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有
5、已知:如图,梯形ABCD中,AD∥BC,AB=DC,AC、BD相交于点O,那么,图中全等三角形共有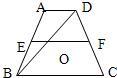 10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( )
10、如图,梯形ABCD中,AD∥BC,BD为对角线,中位线EF交BD于O点,若FO-EO=3,则BC-AD等于( ) 如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,
如图,梯形ABCD中,已知AD∥BC,∠A=90°,AB=7,AD=2,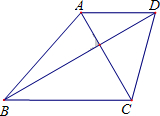 如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.
如图,梯形ABCD中,AD∥BC,BC=5,AD=3,对角线AC⊥BD,且∠DBC=30°,求梯形ABCD的高.