题目内容
已知样本a,4,3,5,2的平均数是b,且a、b是方程x2-4x+3=0的两个根,则这个样本的方差为分析:先解方程求出a、b的值,然后根据方差的计算公式去求方差.方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2].
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
解答:解:已知方程x2-4x+3=0,解方程得x1=1,x2=3;
∵a、b是方程x2-4x+3=0的两个根,
又∵样本中其他数据都大于1,
∴a=1,b=3.
则S2=
[(1-3)2+(4-3)2+(2-3)2+(5-3)2+(3-3)2]=2.
故答案为2.
∵a、b是方程x2-4x+3=0的两个根,
又∵样本中其他数据都大于1,
∴a=1,b=3.
则S2=
| 1 |
| 5 |
故答案为2.
点评:本题将解方程和求方差进行综合考查,解题时重点是要考虑a、b的取值情况.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
已知样本x1,x2,…,xn的方差是2,则样本3x1+5,3x2+5,…,3xn+5的方差是( )
| A、11 | B、18 | C、23 | D、36 |
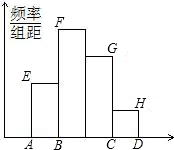 已知样本容量为30,在以下样本频率分布直方图中,各小长方形的高之比AE:BF:CG:DH=2:4:3:1,则第2组的频率和频数分别为
已知样本容量为30,在以下样本频率分布直方图中,各小长方形的高之比AE:BF:CG:DH=2:4:3:1,则第2组的频率和频数分别为