题目内容
【题目】(材料阅读)数轴是数学学习的一个很重要的工具，利用数轴可以将数与形完美结合.通过数轴我们可发现许多重要的规律：
①对值的几何意义：一般地，若点
、点
在数轴上表示的有理数分别为
，
，那么、两点之间的距离表示为
，记作
，
则表示数
和1在数轴上对应的两点之间的距离；又如
，所以
表示数和
在数轴上对应的两点之间的距离；
②若数轴上点、点表示的数分别为、，那么线段
的中点
表示的数为
.
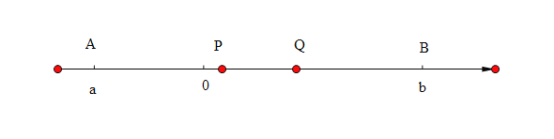
(问题情境)如图，在数轴上，点表示的数为
，点在原点右侧，表示的数为，动点
从点出发以每秒
个单位长度的速度沿数轴正方向运动，同时，动点
从点出发以每秒个单位长度的速度沿数轴负方向运动，其中线段
的中点记作点.
(综合运用)
(1)出发
秒后，点和点相遇，则表示的数
___________；
(2)在第(1)问的基础上，当
时，求运动时间；
(3)在第(1)问的基础上，点、在相遇后继续以原来的速度在这条数轴上运动，但、两点运动的方向相同.随着点、的运动，线段的中点也相应移动，问线段的中点能否与表示
的点重合？若能，求出从、相遇起经过的运动时间；若不能，请说明理由.
【答案】（1）
；
（2）8秒或者16秒；
（3）
能与表示
的点重合，
秒.
【解析】
（1）根据题意即可得到结论；
（2）由（1）可知点
和点
在点A与B上运动时相遇的时间是12秒，求出、两点在
上运动，相遇的时间
，则可以利用两个相遇时间的差，得出没相遇时，满足
的时间，或者利用两个相遇时间的和，得出相遇后，点和点继续运动，满足时的时间；
（3）当线段的中点与表示的点重合时，点和点向数轴的负方向运动，设点表示的数是x，点表示的数是y，由此可得
，并根据中点的数的表示公式
，化简求值即可.
解：（1）依题意得：
，并且
，
则有
，
，
∴
，
∴
，
（2）
如图示：
∵
∴设、两点在上运动，相遇的时间是，则，
依题意得：
，
解之得：
，
由（1）可知，在
上出发
秒后，点和点相遇，
∴当点和点没相遇时，使，
时间为：
，
当点和点相遇又分开时，使，
时间为：
，
即：出发8秒或者16秒后，，
（3）能与表示的点重合，
线段的中点与表示的点重合时，点和点向数轴的负方向运动，
如图示：
点和点在C点相遇，
∴
，
∴点C 表示的数是4，
设点表示的数是x，点表示的数是y，
则依题意得：，
化简得：
，
并且，根据中点的数的表示公式可得：，
即有：
，代入，
则可得：
，
∴
，
∴当线段的中点是表示的点时，从、相遇起经过的运动时间为：
（秒），
