题目内容
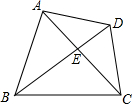（2012•闸北区一模）已知：如图，在四边形ABCD中，BD平分∠ABC，与AC交于点E，AD2=BD•ED．（1）求证：△ADE∽△BDA
（2）如果BA=10，BC=12，BD=15，求BE的长．
分析：（1）根据AD2=BD•ED得出
=
，再根据∠ADE=∠BDA，即可证出△AED∽△BDA．
（2）根据△AED∽△BDA，得出∠AED=∠BAD，再通过证明△EBC∽△ABD，得出
=
，再把BA、BC、BD的值代入即可求出BE的长．
| AD |
| ED |
| BD |
| AD |
（2）根据△AED∽△BDA，得出∠AED=∠BAD，再通过证明△EBC∽△ABD，得出
| BC |
| BD |
| BE |
| BA |
解答：解：（1）证明：∵AD2=BD•ED，
∴
=
，
∵∠ADE=∠BDA，
∴△AED∽△BDA．
（2）∵△AED∽△BDA，
∴∠AED=∠BAD．
∵∠BEC=∠AED，
∴∠BEC=∠BAD．
∵BD平分∠ABC，即∠EBC=∠ABD，
∴△EBC∽△ABD．
∴
=
．
∵BA=10，BC=12，BD=15，
∴
=
，
∴BE=8．
∴
| AD |
| ED |
| BD |
| AD |
∵∠ADE=∠BDA，
∴△AED∽△BDA．
（2）∵△AED∽△BDA，
∴∠AED=∠BAD．
∵∠BEC=∠AED，
∴∠BEC=∠BAD．
∵BD平分∠ABC，即∠EBC=∠ABD，
∴△EBC∽△ABD．
∴
| BC |
| BD |
| BE |
| BA |
∵BA=10，BC=12，BD=15，
∴
| 12 |
| 15 |
| BE |
| 10 |
∴BE=8．
点评：此题考查了相似三角形的判定与性质；关键是综合利用三角形的判定与性质列出比例式求出线段的长．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目