题目内容
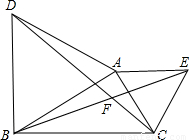
已知△ABD和△ACE都是等边三角形,CD,BE相交于点F.(1)求证:△ABE≌△ADC.
(2)图中哪两个三角形可以通过怎样的旋转而相互得到?
(3)求∠BFC的度数.
【答案】分析:(1)根据全等三角形的SAS定理,即可证得;
(2)由(1)可知,△ABE≌△ADC,只需找出旋转角,即可得出;
(3)根据等边三角形的性质和全等三角形的性质,可得∠BDF+∠ABE=60°,继而可求出∠BFD=60°,同理可得∠CFE=60°,根据周角及对顶角的性质,即可求出;
解答:(1)证明:∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠CAD=∠EAB,
在△ABE和△ADC中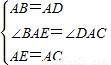 ,
,
∴△ABE≌△ADC;
(2)解:由图可知,△ABE绕点A顺时针旋转60°,可得到△ADC;
(3)解:∵△ABE≌△ADC,
∴∠ABE=∠ADC,
∵∠BDF+∠ADC=60°,
∴∠BDF+∠ABE=60°,
∴∠BFD=180°-∠ABD-(∠BDF+∠ABE)=60°,
同理可得,∠CFE=60°,
∴∠BFC=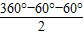 =120°.
=120°.
点评:本题主要考查了等边三角形的性质、全等三角形的判定与性质和旋转的知识,本题需要用到的知识点比较多,考查了学生对于知识的综合运用能力.
(2)由(1)可知,△ABE≌△ADC,只需找出旋转角,即可得出;
(3)根据等边三角形的性质和全等三角形的性质,可得∠BDF+∠ABE=60°,继而可求出∠BFD=60°,同理可得∠CFE=60°,根据周角及对顶角的性质,即可求出;
解答:(1)证明:∵△ABD和△ACE都是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠CAD=∠EAB,
在△ABE和△ADC中
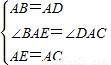 ,
,∴△ABE≌△ADC;
(2)解:由图可知,△ABE绕点A顺时针旋转60°,可得到△ADC;
(3)解:∵△ABE≌△ADC,
∴∠ABE=∠ADC,
∵∠BDF+∠ADC=60°,
∴∠BDF+∠ABE=60°,
∴∠BFD=180°-∠ABD-(∠BDF+∠ABE)=60°,
同理可得,∠CFE=60°,
∴∠BFC=
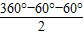 =120°.
=120°.点评:本题主要考查了等边三角形的性质、全等三角形的判定与性质和旋转的知识,本题需要用到的知识点比较多,考查了学生对于知识的综合运用能力.

练习册系列答案
相关题目
 19、如图,在已知△ABC和△BAD中有以下四个判断:①AD=BC;②AC=BD;③∠C=∠D;④∠BAC=∠ABD.请你从中选择两个作为条件、一个作为结论,写出一个真命题并加以证明.
19、如图,在已知△ABC和△BAD中有以下四个判断:①AD=BC;②AC=BD;③∠C=∠D;④∠BAC=∠ABD.请你从中选择两个作为条件、一个作为结论,写出一个真命题并加以证明.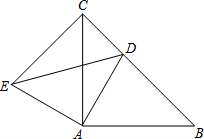 (2013•南通一模)已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点.
(2013•南通一模)已知△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D为BC边上一点. 如图,已知△ABD和△ACE,AD=AE,∠1=∠2,要判定△ABD≌△ACE,还需要添加一个条件,这个条件可以是
如图,已知△ABD和△ACE,AD=AE,∠1=∠2,要判定△ABD≌△ACE,还需要添加一个条件,这个条件可以是