题目内容
已知双曲线: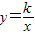 与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点.
与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点.(1)求双曲线与抛物线的解析式;
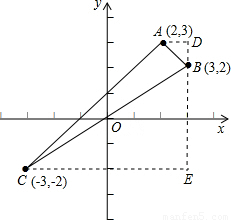
(2)在平面直角坐标系中描出点A、点B、点C,并求出△ABC的面积.
【答案】分析:(1)函数图象过某一点时,这点就满足关系式,利用待定系数法分别求出反比例函数与二次函数解析式即可;
(2)根据A,B,C三点的坐标可以得出△ADB,△BCE和梯形ADEC的面积,用梯形面积减去两三角形面积即可得到△ABC的面积.
解答:解:(1)把点A(2,3)代入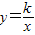 得:k=6,
得:k=6,
∴y=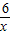 ,
,
把B(m,2)、C(-3,n)分别代入y=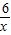 得,
得,
m=3,n=-2,
把A(2,3)、B(3,2)、C(-3,-2)分别代入y=ax2+bx+c得:
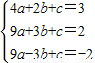 ,
,
解得: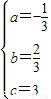 ,
,
∴抛物线的解析式为:y=- x2+
x2+ x+3;
x+3;
(2)描点画图得:
S△ABC=S梯形ADEC-S△ADB-S△BCE,
= (1+6)×5-
(1+6)×5- ×1×1-
×1×1- ×6×4,
×6×4,
=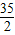 -
- -12,
-12,
=5.
点评:此题主要考查了二次函数的综合应用以及待定系数法求函数解析式,二次函数的综合应用是初中阶段的重点题型特别注意利用数形结合是这部分考查的重点也是难点同学们应重点掌握.
(2)根据A,B,C三点的坐标可以得出△ADB,△BCE和梯形ADEC的面积,用梯形面积减去两三角形面积即可得到△ABC的面积.
解答:解:(1)把点A(2,3)代入
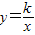 得:k=6,
得:k=6,∴y=
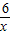 ,
,把B(m,2)、C(-3,n)分别代入y=
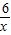 得,
得,m=3,n=-2,
把A(2,3)、B(3,2)、C(-3,-2)分别代入y=ax2+bx+c得:
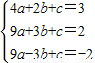 ,
,解得:
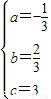 ,
,
∴抛物线的解析式为:y=-
 x2+
x2+ x+3;
x+3;(2)描点画图得:
S△ABC=S梯形ADEC-S△ADB-S△BCE,
=
 (1+6)×5-
(1+6)×5- ×1×1-
×1×1- ×6×4,
×6×4,=
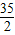 -
- -12,
-12,=5.
点评:此题主要考查了二次函数的综合应用以及待定系数法求函数解析式,二次函数的综合应用是初中阶段的重点题型特别注意利用数形结合是这部分考查的重点也是难点同学们应重点掌握.

练习册系列答案
相关题目
 与抛物线y=ax2+bx+c交于A(2,3)、B(m,2)、c(-3,n)三点.
与抛物线y=ax2+bx+c交于A(2,3)、B(m,2)、c(-3,n)三点. 已知双曲线y=
已知双曲线y=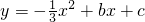 交于A(2,3)、B(m,2)三点.
交于A(2,3)、B(m,2)三点. 与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点.
与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点.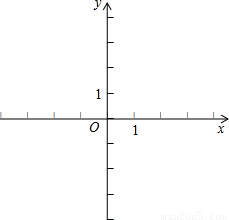
 与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点.
与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点.