题目内容
 已知双曲线y=
已知双曲线y= 与抛物线
与抛物线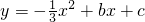 交于A(2,3)、B(m,2)三点.
交于A(2,3)、B(m,2)三点.
(1)求双曲线与抛物线的解析式;
(2)在平面直角坐标系中描出点A、点B,并求出△ABO的面积.
 解:(1)把A(2,3)和B(m,2)代入y=
解:(1)把A(2,3)和B(m,2)代入y= 得k=2×3=m×2,
得k=2×3=m×2,解得k=6,m=3,
所以反比例函数解析式为y=
 ;
;把A(2,3)和B(3,2)代入y=-
 x2+bx+c得
x2+bx+c得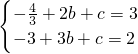 ,解得
,解得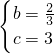 ,
,所以抛物线的解析式入y=-
 x2+
x2+ x+3;
x+3;(2)作AC⊥x轴于C,BD⊥x轴于D,如图,
S△OAB=S△OAC+S梯形ABDC-S△OBD
=
 ×2×3+
×2×3+ ×(2+3)×1-
×(2+3)×1- ×3×2
×3×2=
 .
.分析:(1)直接把A点和B点坐标代入反比例函数解析式可求出k与m,从而确定反比例解析式和B点坐标,然后把A、B两点坐标代入二次函数解析式得到关于b、c的方程组,解方程组求出b、c即可得到抛物线的解析式;
(2)利用S△OAB=S△OAC+S梯形ABDC-S△OBD进行计算.
点评:本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
 已知双曲线:
已知双曲线: 与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点.
与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点. 与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点.
与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点.
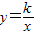 与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点.
与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点.