题目内容
已知双曲线y= 与抛物线y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点,请你求出双曲线与抛物线的解析式.
与抛物线y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点,请你求出双曲线与抛物线的解析式.
解:把点A的坐标代入反比例函数得, =3,
=3,
解得k=6,
所以,反比例函数解析式为y= ;
;
把点B(m,2)、C(-3,n)坐标代入反比例函数解析式得,
 =2,
=2, =n,
=n,
解得m=3,n=-2,
所以,点B(3,2)、C(-3,-2),
把点A、B、C代入抛物线解析式得,
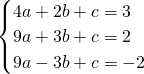 ,
,
解得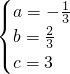 .
.
所以,抛物线解析式为y=- x2+
x2+ x+3.
x+3.
分析:把点A的坐标代入反比例函数解析式求出k的值,从而得到反比例函数解析式,再把点B、C的坐标代入反比例函数解析式求出m、n的值,从而得到点B、C,再利用待定系数法求二次函数解析式即可.
点评:本题考查了待定系数法求抛物线解析式,反比例函数图象上点的特征,求出点B、C的坐标是解题的关键.
 =3,
=3,解得k=6,
所以,反比例函数解析式为y=
 ;
;把点B(m,2)、C(-3,n)坐标代入反比例函数解析式得,
 =2,
=2, =n,
=n,解得m=3,n=-2,
所以,点B(3,2)、C(-3,-2),
把点A、B、C代入抛物线解析式得,
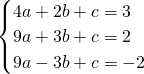 ,
,解得
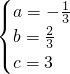 .
.所以,抛物线解析式为y=-
 x2+
x2+ x+3.
x+3.分析:把点A的坐标代入反比例函数解析式求出k的值,从而得到反比例函数解析式,再把点B、C的坐标代入反比例函数解析式求出m、n的值,从而得到点B、C,再利用待定系数法求二次函数解析式即可.
点评:本题考查了待定系数法求抛物线解析式,反比例函数图象上点的特征,求出点B、C的坐标是解题的关键.

练习册系列答案
相关题目
 与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点.
与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点.
 与抛物线y=ax2+bx+c交于A(2,3)、B(m,2)、c(-3,n)三点.
与抛物线y=ax2+bx+c交于A(2,3)、B(m,2)、c(-3,n)三点.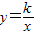 与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点.
与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点.
 与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点.
与抛物线:y=ax2+bx+c交于A(2,3)、B(m,2)、C(-3,n)三点.