题目内容
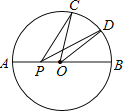
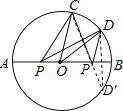
【题目】如图,已知⊙O的半径为2,C、D是直径AB同侧圆周上的两点,弧AC的度数是100°,D为弧BC的中点,动点P在直径AB上,则PC+PD的最小值是 .
【答案】2![]()
【解析】
试题分析:作点D关于AB的对称点D′,连接CD′与AB的交点即为所求的点P,CD′的长度为PC+PD的最小长度,求出弧BC的度数,再求出弧BD的度数,从而得到弧CD′的度数,连接OD′,过点O作OE⊥CD′,然后根据垂径定理求解即可.
解:如图,作点D关于AB的对称点D′,连接CD′,
由轴对称确定最短路线问题,CD′与AB的交点即为所求的点P,CD′的长度为PC+PD的最小长度,
∵弧AC的度数为100°,
∴弧BC的度数为180°﹣100°=80°,
∵弧BC=2弧BD,
∴弧BD的度数=![]() ×80°=40°,
×80°=40°,
∴弧CD′的度数=80°+40°=120°,
连接OD′,过点O作OE⊥CD′,
则∠COD′=120°,OE垂直平分CD′,
∴CD′=2CE=2×![]() ×2=2
×2=2![]() .
.
∴PC+PD的最小值是2![]() .
.
故答案为:2![]() .
.

练习册系列答案
相关题目
【题目】某旅游景点的门票价格如下表:
购票人数/人 | 1﹣50 | 51﹣100 | 100以上 |
每人门票价/元 | 80 | 75 | 70 |
某校八年级(1)、(2)两班共100多人计划去游览该景点,其中(1)班人数少于50人,(2)班人数有50多人,如果两班都以班为单位单独购票,则一共支付7965元;如果两班联合起来作为一个团体购票,则只需花费7210元.两个班各有多少名学生?