题目内容
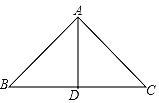
【题目】如图,在△ABC中,AB=AC=2,BC=![]() ,且∠BAC=120°,点D是线段BC上的一动点(不与点B、C重合),连接AD,作∠ADE=30°,DE交AC于点E.
,且∠BAC=120°,点D是线段BC上的一动点(不与点B、C重合),连接AD,作∠ADE=30°,DE交AC于点E.
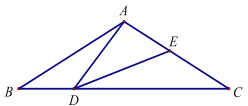
(1)求证:∠BAD∠EDC;
(2)当BD= 时,△ABD≌△EDC,并说明理由.
(3)当△ADE是直角三角形时,求AD的长?
【答案】(1)证明见解析;(2)答案见解析;(3)![]() 或1
或1
【解析】
(1)根据等腰三角形的性质及三角形内角和定理得出∠B=30°,然后根据三角形外角的性质即可得出结论;
(2)先求出DC的长,可得到AB=DC.根据ASA即可证明△ABD≌△EDC;
(3)分两种情况讨论:①当∠DAE=90°时,△CAD是含30°角的直角三角形,可得出AC=![]() AD=2,求出AD的长即可.
AD=2,求出AD的长即可.
②当∠DEA=90°时,∠DAE=∠BAD=60°,得到△ABD是含30°角的直角三角形,即可得到AD的长.
(1)∵∠BAC=120°,AB=AC,∴∠B=∠C=30°.
又∵∠ADC=∠B+∠BAD,∴∠ADE+∠EDC=∠B+∠BAD.
又∵∠ADE=30°,∴∠BAD=∠EDC.
(2)当BD=![]() 时,△ABD≌△EDC.理由如下:
时,△ABD≌△EDC.理由如下:
∵BD=![]() ,BC=
,BC=![]() ,∴DC=
,∴DC=![]() =2,∴AB=DC.
=2,∴AB=DC.
在△ABD和△EDC中,∵∠B=∠C,AB=DC,∠BAD=∠EDC,∴△ABD≌△EDC.
(3)①当∠DAE=90°时.
∵∠C=30°,∴AC=![]() AD=2,∴AD=
AD=2,∴AD=![]() =
=![]() .
.
②当∠DEA=90°时,∠DAE=∠BAD=60°.
又∵∠B=30°,∴∠ADB=90°,∴AD=![]() AB=1.
AB=1.
综上所述:当△ADE 是直角三角形时,AD=![]() 或1.
或1.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目