题目内容
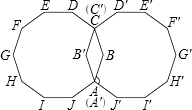 如图平面上有两个全等的正十边形ABCDEFGHIJ、A′B′C′D′E′F′G′H′I′J′,其中A点与A′点重合,C点与C′点重合.求∠BAJ′的度数为何?( )
如图平面上有两个全等的正十边形ABCDEFGHIJ、A′B′C′D′E′F′G′H′I′J′,其中A点与A′点重合,C点与C′点重合.求∠BAJ′的度数为何?( )| A、96 | B、108 | C、118 | D、126 |
分析:利用正多边形的性质可以得到四边形ABCB′为菱形,计算其内角后,用多边形的内角减去即可得到答案.
解答:解题技巧:(1)正n边形每一个内角度数=
,(2)菱形的邻角互补
[解析]∵两个图形为全等的正十边形,
∴ABCB′为菱形,
又∠ABC=∠AB′C=
=144°
∴∠BAB′=180°-144°=36°,
?∠BAJ′=∠B′AJ′-∠BAB′
=144°-36°
=108°.
故选B.
| 180°×(n-2) |
| n |
[解析]∵两个图形为全等的正十边形,
∴ABCB′为菱形,
又∠ABC=∠AB′C=
| 180°×(10-2) |
| 10 |
∴∠BAB′=180°-144°=36°,
?∠BAJ′=∠B′AJ′-∠BAB′
=144°-36°
=108°.
故选B.
点评:本题考查了正多边形与圆的计算,解题的关键是利用正多边形的性质判定菱形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
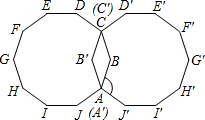 (2012•鼓楼区二模)如图,平面上有两个全等的正十边形,其中A点与A′点重合,C点与C′点重合.∠BAJ′为
(2012•鼓楼区二模)如图,平面上有两个全等的正十边形,其中A点与A′点重合,C点与C′点重合.∠BAJ′为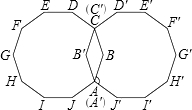 如图平面上有两个全等的正十边形ABCDEFGHIJ、A′B′C′D′E′F′G′H′I′J′,其中A点与A′点重合,C点与C′点重合.求∠BAJ′的度数为何?
如图平面上有两个全等的正十边形ABCDEFGHIJ、A′B′C′D′E′F′G′H′I′J′,其中A点与A′点重合,C点与C′点重合.求∠BAJ′的度数为何?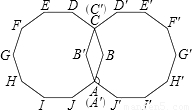
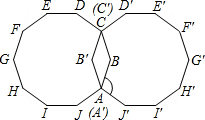 如图,平面上有两个全等的正十边形,其中A点与A′点重合,C点与C′点重合.∠BAJ′为________°.
如图,平面上有两个全等的正十边形,其中A点与A′点重合,C点与C′点重合.∠BAJ′为________°.