题目内容
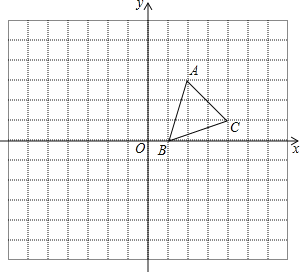
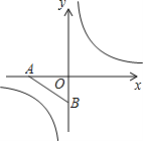
【题目】在平面直角坐标系中,已知点A、B的坐标分别为(-![]() ,0)、(0,-1),把点A绕坐标原点O顺时针旋转135°得点C,若点C在反比例函数y=
,0)、(0,-1),把点A绕坐标原点O顺时针旋转135°得点C,若点C在反比例函数y=![]() 的图象上.
的图象上.
(1)求反比例函数的表达式;
(2)若点D在y轴上,点E在反比例函数y=![]() 的图象上,且以点A、B、D、E为顶点的四边形是平行四边形.请画出满足题意的示意图并在示意图的下方直接写出相应的点D、E的坐标.
的图象上,且以点A、B、D、E为顶点的四边形是平行四边形.请画出满足题意的示意图并在示意图的下方直接写出相应的点D、E的坐标.
【答案】(1)y=![]() ;(2)示意图见解析,E(-
;(2)示意图见解析,E(-![]() ,-
,-![]() ),D(0,-1-
),D(0,-1-![]() )或E(-
)或E(-![]() ,-
,-![]() ),D(0,-1+
),D(0,-1+![]() )或E
)或E 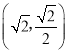 , D
, D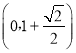
【解析】
(1)根据旋转和直角三角形的边角关系可以求出点C的坐标,进而确定反比例函数的关系式;
(2)分两种情况进行讨论解答,①点E在第三象限,由题意可得E的横坐标与点A的相同,将A的横坐标代入反比例函数的关系式,可求出纵坐标,得到E的坐标,进而得到AE的长,也是BD的长,因此D在B的上方和下方,即可求出点D的坐标,②点E在第一象限,由三角形全等,得到E的横坐标,代入求出纵坐标,确定E的坐标,进而求出点D的坐标.
(1)由旋转得:OC=OA=![]() ,∠AOC=135°,
,∠AOC=135°,
过点C作CM⊥y轴,垂足为M,则∠COM=135°-90°=45°,
在Rt△OMC中,∠COM=45°,OC=![]() ,
,
∴OM=CM=1,
∴点C(1,1),代入y=![]() 得:k=1,
得:k=1,
∴反比例函数的关系式为:y=![]() ,
,
答:反比例函数的关系式为:y=![]()
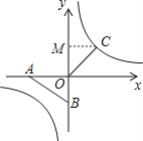
(2)①当点E在第三象限反比例函数的图象上,如图1,图2,
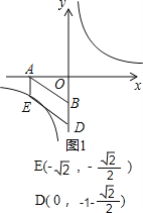
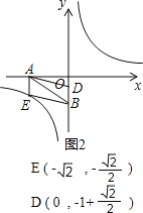
∵点D在y轴上,AEDB是平行四边形,
∴AE∥DB,AE=BD,AE⊥OA,
当x=-![]() 时,y=
时,y=![]() =-
=-![]() ,
,
∴E(-![]() ,-
,-![]() )
)
∵B(0,-1),BD=AE=![]() ,
,
当点D在B的下方时,
∴D(0,-1-![]() )
)
当点D在B的上方时,
∴D(0,-1+![]() ),
),
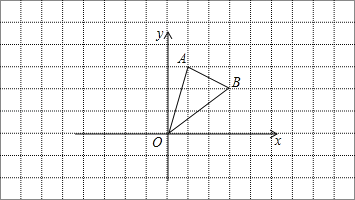
②当点E在第一象限反比例函数的图象上时,如图3,
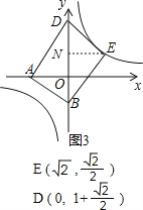
过点E作EN⊥y轴,垂足为N,
∵ABED是平行四边形,
∴AB=DE,AB=DE,
∴∠ABO=∠EDO,
∴△AOB≌△END (AAS),
∴EN=OA=![]() ,DN=OB=1,
,DN=OB=1,
当x=![]() 时,代入y=
时,代入y=![]() 得:y=
得:y=![]() ,
,
∴E(![]() ,
,![]() ),
),
∴ON=![]() ,OD=ON+DN=1+
,OD=ON+DN=1+![]() ,
,
∴D(0,1+![]() )
)

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案【题目】甲、乙两台机床同时加工直径为![]() 的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取
的同种规格零件,为了检查两台机床加工零件的稳定性,质检员从两台机床的产品中各抽取![]() 件进行检测,结果如下(单位:
件进行检测,结果如下(单位:![]() ):
):
甲 |
|
|
|
|
|
乙 |
|
|
|
|
|
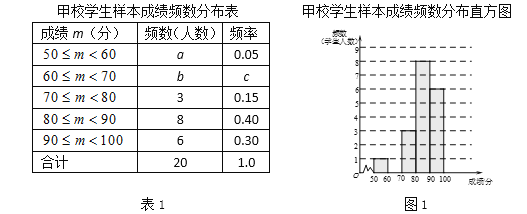
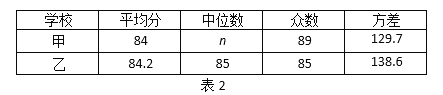
(1)分别求出这两台机床所加工零件直径的平均数和方差;
(2)根据所学的统计知识,你认为哪一台机床生产零件的稳定性更好一些,说明理由.