题目内容
一条直线可以把一个平面分成两部分,两条直线可以把一个平面分成四部分,那么三条直线最多可以把一个平面分成几部分?四条直线呢?你能发现什么规律?
分析:作出三条直线、四条直线相交的情况,然后查出分成平面的部分数,再根据数据特点确定出变化规律即可得解.
解答: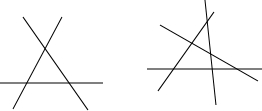 解:一条直线把一个平面分成2部分,
解:一条直线把一个平面分成2部分,
两条直线可以把一个平面分成4部分,
三条直线可以把一个平面分成7部分,
四条直线可以把一个平面分成11部分,
…,
设a1=2,a2=4,a3=7,a4=11,…,
则a2-a1=2,
a3-a2=3,
a4-a3=4,
a5-a4=5,
…,
an-an-1=n,
所以,an=2+2+3+4+5+…+n=1+1+2+3+4+5+…+n=
+1,
故,n条直线可以把一个平面分成
+1部分.
 解:一条直线把一个平面分成2部分,
解:一条直线把一个平面分成2部分,两条直线可以把一个平面分成4部分,
三条直线可以把一个平面分成7部分,
四条直线可以把一个平面分成11部分,
…,
设a1=2,a2=4,a3=7,a4=11,…,
则a2-a1=2,
a3-a2=3,
a4-a3=4,
a5-a4=5,
…,
an-an-1=n,
所以,an=2+2+3+4+5+…+n=1+1+2+3+4+5+…+n=
| n(n+1) |
| 2 |
故,n条直线可以把一个平面分成
| n(n+1) |
| 2 |
点评:本题考查了直线、射线、线段的知识,判断出相邻直线条数分成平面的部分的差是连续的自然数是解题的关键.

练习册系列答案
相关题目
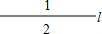 (1)一条直线可以把平面分成两个部分(或区域),如图,两条直线可以把平面分成几个部分?三条直线可以把平面分成几个部分?试画图说明.
(1)一条直线可以把平面分成两个部分(或区域),如图,两条直线可以把平面分成几个部分?三条直线可以把平面分成几个部分?试画图说明. ×BC×AF,S△BCD=
×BC×AF,S△BCD=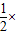 BC×DE
BC×DE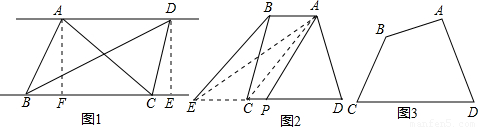
 ×BC×AF,S△BCD=
×BC×AF,S△BCD=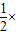 BC×DE
BC×DE