题目内容
(1)一条直线可以把平面分成两部分,如图所示,两条直线可以把平面分面几个部分?三条直线可以把平面分成几个部分?试画图说明.
(2)四条直线最多可以把平面分成几个部分?试画出示意图,并说明这四条直线的位置关系.
(3)平面上有n条直线,每两条直线都恰好相交,且没有三条直线交于点一点,处于这种位置的n条直线分一个平面所成的区域最多,记为an,试写出an与n之间的关系.
答案:
解析:
解析:
|
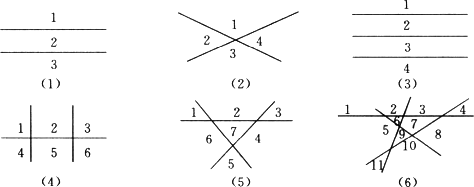
解决本题应用在图形的基础上得出答案,重在考查学生的作图能力,同时,本题还是探索规律题,应掌握从特殊到一般的思考方法. (1)两条直线因其相互位置不同,可以把平面分成3个或4个部分,如图(1)(2)所示.
三条直线因其相互位置不同,可以把平面分成4个、6个或7个部分,如图(3)(4)(5)所示. (2)四条直线最多可以把平面分成11个部分,如图(6)所示,此时这四条直线的位置关系是两两相交,且无三线共点. (3)不在是n条直线两两相交,且没有三条直线交于一点,把平面分成an个部分. ①当n=1时,a1=2=1+1; ②当n=2时,a2=4=1+1+2; ③当n=3时,a3=7=1+1+2+3; ④当n=4时,a4=11=1+1+2+3+4; …… 由此可归纳出公式: an=1+(1+2+3+4+…+n) = = |

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
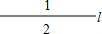 (1)一条直线可以把平面分成两个部分(或区域),如图,两条直线可以把平面分成几个部分?三条直线可以把平面分成几个部分?试画图说明.
(1)一条直线可以把平面分成两个部分(或区域),如图,两条直线可以把平面分成几个部分?三条直线可以把平面分成几个部分?试画图说明.