题目内容
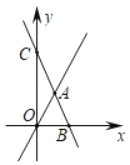
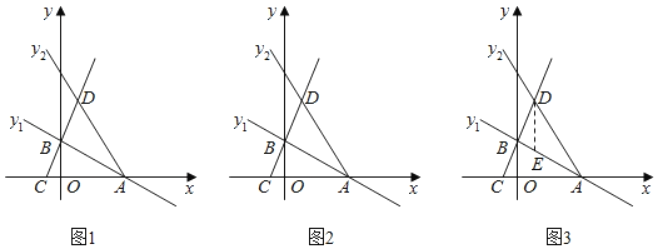
【题目】如图1,平面直角坐标系中,直线y1=﹣![]() x+3与x轴、y轴分别交于A、B两点,直线y2=﹣2x+b经过点A,已知点C(﹣1,0),直线BC与直线y2相交于点D.
x+3与x轴、y轴分别交于A、B两点,直线y2=﹣2x+b经过点A,已知点C(﹣1,0),直线BC与直线y2相交于点D.
(1)请直接写出:A点坐标为 ,直线BC解析式为 ,D点坐标为 ;
(2)若线段OA在x轴上移动,且点O,A移动后的对应点为O1、A1,首尾顺次连接点O1、A1、D、B构成四边形O1A1DB,当四边形O1A1DB的周长最小时,y轴上是否存在点M,使|A1M﹣DM|有最大值,若存在,请求出此时M的坐标;若不存在请说明理由.
(3)如图3,过点D作DE∥y轴,与直线AB交于点E,若Q为线段AD上一动点,将△DEQ沿边EQ翻折得到直线AB上方的△D′EQ,是否存在点Q使得△D′EQ与△AEQ的重叠部分图形为直角三角形,若存在,请求出DQ的长;若不存在,请说明理由.
【答案】(1)(4,0),y=3x+3,(1,6);(2)M(0,9);(3)![]() 或
或![]() .
.
【解析】
(1)利用坐标轴上点的特点求出点A,B坐标,进而利用待定系数法求出直线AD的解析式,联立两直线解析式求解即可得出点D坐标;
(2)利用对称性和平行四边形的性质找出四边形O1A1DB的周长最小时点A1的位置,再利用待定系数法求出直线DG的解析式,即可得出结论;
(3)分两种情况,先求出DE,再利用锐角三角函数求出EF,进而利用勾股定理求出DF,再利用角平分线的性质,求出DN,最后利用相似三角形的性质得出比例式,建立方程求解即可.
解:(1)对于直线y1=﹣![]() x+3,令x=0,则y=3,
x+3,令x=0,则y=3,
∴B(0,3),令y=0,则0=﹣![]() x+3,
x+3,
∴x=4,
∴A(4,0),
∵直线y2=﹣2x+b经过点A,
∴﹣2×4+b=0,
∴b=8,
∴直线y2=﹣2x+8①,
设直线BC的解析式为![]() mx+n,
mx+n,
∵C(﹣1,0),
∴![]() ,
,
∴![]() ,
,
∴直线BC的解析式为y=3x+3②,
联立①②解得,![]() ,
,
∴D(1,6),
故答案为:(4,0),y=3x+3,(1,6);
(2)如图1,
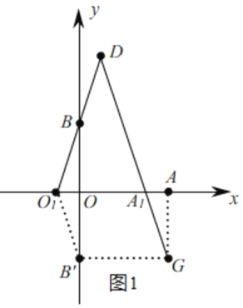
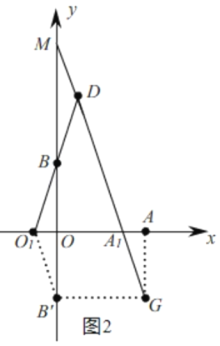
作点B关于x轴的对称点B'(0,﹣3),以OA与OB'为边作OB'GA,
∴B'G=OA,
∵∠AOB'=90°,
∴OB'GA是矩形,
∴G(4,﹣3),
连接DG,向左平移OA使点A落在DG与x轴的交点上,记作A1,连接O1B',
此时四边形O1A1DB的周长最小,
设直线DG的解析式为y=kx+a,
∵D(1,6),
∴![]() ,
,
∴![]() ,
,
span>∴直线DG的解析式为y=﹣3x+9,
要|A1M﹣DM|有最大值,则点M是DG与y轴的交点,如图2,
∴M(0,9);
(3)∵DE∥y轴,D(1,6),
∴E(1,![]() ),
),
∴DE=![]() ,
,
由折叠知,ED'=DE=![]() ,∠DEQ=∠FEQ,
,∠DEQ=∠FEQ,
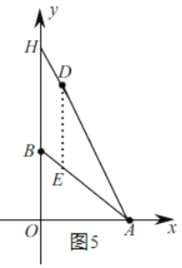
如图5,设直线AD交y轴于H,
∵点A(4,0),D(1,6),
∴直线AD的解析式为y=﹣2x+8,
∴H(0,8),
在Rt△AOH中,tan∠AHO=![]() ,=
,=![]() ,
,
∵DE∥y轴,
∴∠ADE=∠AHO,
∴tan∠ADE=![]() ,
,
设EE'与AD的交点为F,
①当∠DFE=90°时,如图3,
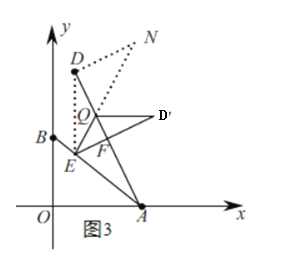
在Rt△DFE中,tan∠ADE=![]() =
=![]() ,
,
∴DF=2EF,根据勾股定理得,EF2+(2EF)2=(![]() )2,
)2,
∴EF=![]() ,DF=
,DF=![]() ,
,
过点D作DN∥EE'交EQ的延长线于N,
∴∠FEQ=∠N,
∴∠DEQ=∠N,
∴DN=DE=![]() ,
,
∵DN∥EF,
∴△QFE∽△QDN,
∴![]() ,
,
∴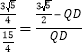 ,
,
∴DQ=![]() ,
,
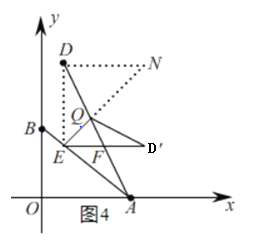
②当∠DEF=90°时,如图4,过点D作DN∥EF交EQ的延长线于N,
在Rt△DEF中,tan∠ADE=![]() =
=![]() ,
,
∴EF=![]() DE=
DE=![]() ,根据勾股定理得,DF=
,根据勾股定理得,DF=![]() ,
,
同①的方法得,DN=DE=![]() ,
,
∵DN∥EF,
∴△QFE∽△QDN,
∴![]() ,
,
∴ ,
,
∴QD=![]() .
.
即:DQ的长为![]() 或
或![]() .
.
故答案为:(1)(4,0),y=3x+3,(1,6);(2)M(0,9);(3)![]() 或
或![]() .
.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案