题目内容
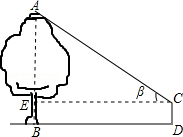
小亮和小红在公园放风筝,不小心让风筝挂在树梢上,风筝固定在A处(如图),为测量此时风筝的高度,他俩按如下步骤操作:
第一步:小亮在测点D处用测角仪测得仰角 。
。
第二步:小红量得测点D处到树底部B的水平距离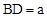 。
。
第三步:量出测角仪的高度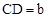 。
。
之后,他俩又将每个步骤都测量了三次,把三次测得的数据绘制成如下的条形统计图和折线统计图。
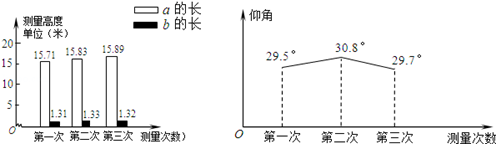
请你根据两个统计图提供的信息解答下列问题。
(1)把统计图中的相关数据填入相应的表格中:
(2)根据表中得到的样本平均值计算出风筝的高度AB(参考数据: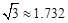 ,
, ,结果保留3个有效数字)。
,结果保留3个有效数字)。
第一步:小亮在测点D处用测角仪测得仰角
 。
。第二步:小红量得测点D处到树底部B的水平距离
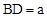 。
。第三步:量出测角仪的高度
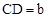 。
。
之后,他俩又将每个步骤都测量了三次,把三次测得的数据绘制成如下的条形统计图和折线统计图。

请你根据两个统计图提供的信息解答下列问题。
(1)把统计图中的相关数据填入相应的表格中:
| | 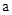 | 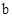 | 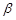 |
| 第一次 | | | |
| 第二次 | | | |
| 第三次 | | | |
| 平均值 | | | |
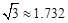 ,
, ,结果保留3个有效数字)。
,结果保留3个有效数字)。解:(1)填写表格如下:
(2)∵四边形EBDC是矩形,∴CE=BD=a,BE=CD=b。
在Rt△AEC中,∵β=30°,a=15.81,
∴AE=BEtan30°=15.81×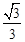 ≈9.128(米)。
≈9.128(米)。
∴AB=AE+EB=9.128+1.32=10.448≈10.4(米)。
答:风筝的高度AB为10.4米。
| | 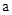 | 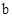 | 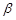 |
| 第一次 | 15.71 | 1.31 | 29.50 |
| 第二次 | 15.83 | 1.33 | 30.80 |
| 第三次 | 15.89 | 1.32 | 29.70 |
| 平均值 | 15.81 | 1.32 | 300 |
在Rt△AEC中,∵β=30°,a=15.81,
∴AE=BEtan30°=15.81×
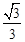 ≈9.128(米)。
≈9.128(米)。∴AB=AE+EB=9.128+1.32=10.448≈10.4(米)。
答:风筝的高度AB为10.4米。
(1)根据图中的信息将数据填入表格,并求平均值即可。
(2)过C作CE⊥AB于E,可知四边形EBDC是矩形,可得CE=BD=a,BE=CD=b,在Rt△AEC中,根据样本平均值a=15.81,β=30°,解直角三角形求出AE的长度,从而可求得树AB的高度,即风筝的高度。
B卷(共30分)
(2)过C作CE⊥AB于E,可知四边形EBDC是矩形,可得CE=BD=a,BE=CD=b,在Rt△AEC中,根据样本平均值a=15.81,β=30°,解直角三角形求出AE的长度,从而可求得树AB的高度,即风筝的高度。
B卷(共30分)

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目

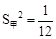 ,乙组数据的方差
,乙组数据的方差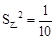 ,下列结论中正确的是
,下列结论中正确的是