题目内容
为培养学生良好学习习惯,某学校计划举行一次“整理错题集”的展示活动,对该校部分学生“整理错题集”的情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.请根据图表中提供的信息,解答下列问题:
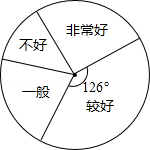
(1)本次抽样共调查了多少学生?
(2)补全统计表中所缺的数据.
(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?
(4)某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.

| 整理情况 | 频数 | 频率 |
| 非常好 | | 0.21 |
| 较好 | 70 | |
| 一般 | | |
| 不好 | 36 | |
(2)补全统计表中所缺的数据.
(3)该校有1500名学生,估计该校学生整理错题集情况“非常好”和“较好”的学生一共约多少名?
(4)某学习小组4名学生的错题集中,有2本“非常好”(记为A1、A2),1本“较好”(记为B),1本“一般”(记为C),这些错题集封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回,从余下的3本错题集中再抽取一本,请用“列表法”或“画树形图”的方法求出两次抽到的错题集都是“非常好”的概率.
解:(1)∵较好的所占的比例是: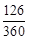 ,
,
∴本次抽样共调查的人数是:70÷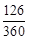 =200(人)。
=200(人)。
(2)填表如下:
(3)该校学生整理错题集情况“非常好”和“较好”的学生一共约有1500×(0.21+0.35)=840(人)。
(4)画树状图如下:
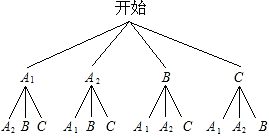
∵共有12种等可能结果,两次抽到的错题集都是“非常好”的情况有2种,
∴两次抽到的错题集都是“非常好”的概率是: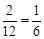 。
。
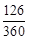 ,
,∴本次抽样共调查的人数是:70÷
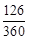 =200(人)。
=200(人)。(2)填表如下:
| 整理情况 | 频数 | 频率 |
| 非常好 | 42 | 0.21 |
| 较好 | 70 | 0.35 |
| 一般 | 52 | 0.26 |
| 不好 | 36 | 0.18 |
(4)画树状图如下:

∵共有12种等可能结果,两次抽到的错题集都是“非常好”的情况有2种,
∴两次抽到的错题集都是“非常好”的概率是:
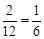 。
。试题分析:(1)根据较好的部分对应的圆心角即可求得对应的百分比,即可求得总数,然后根据频数、频率和总量的关系即可求解。
(2)根据频数、频率和总量的关系即可求解:
非常好的频数是:200×0.21=42(人),一般的频数是:200﹣42﹣70﹣36=52(人),
较好的频率是:
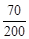 =0.35,一般的频率是:
=0.35,一般的频率是: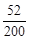 =0.26,不好的频率是:
=0.26,不好的频率是: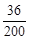 =0.18。
=0.18。(3)利用总人数乘以对应的频率即可。
(4)应用树形图或列表的方法,利用概率公式即可求解。

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 。
。 。
。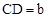 。
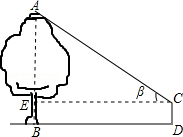
。
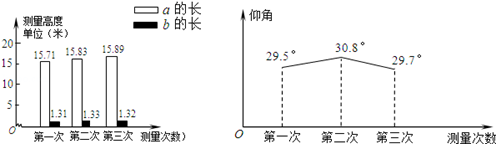
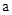
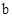
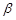
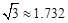 ,
, ,结果保留3个有效数字)。
,结果保留3个有效数字)。 ;C:喝剩约一半;D:开瓶但基本未喝.同学们根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题:
;C:喝剩约一半;D:开瓶但基本未喝.同学们根据统计结果绘制如下两个统计图,根据统计图提供的信息,解答下列问题:

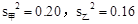 ,则甲、乙两名同学成绩更稳定的是 .
,则甲、乙两名同学成绩更稳定的是 .
 ),这组数据的中位数是【 】
),这组数据的中位数是【 】