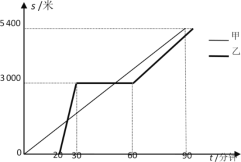
题目内容
【题目】如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧![]() 于点P,Q,且点P, Q在AB异侧,连接OP.
于点P,Q,且点P, Q在AB异侧,连接OP.
(1)求证:AP=BQ;
(2)当BQ=4![]() 时,求扇形COQ的面积及
时,求扇形COQ的面积及![]() 的长(结果保留π);
的长(结果保留π);
(3)若△APO的外心在扇形COD的内部,请直接写出OC的取值范围.

【答案】(1)见解析;(2)![]() ;(3)4<OC<8.
;(3)4<OC<8.
【解析】
试题(1)连接OQ.只要证明Rt△APO≌Rt△BQO即可解决问题;
(2)求出优弧DQ的圆心角以及半径即可解决问题;
(3)由△APO的外心是OA的中点,OA=8,推出△APO的外心在扇形COD的内部时,OC的取值范围为4<OC<8;
试题解析:(1)证明:连接OQ.
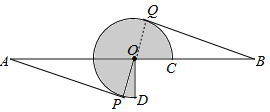
∵AP、BQ是⊙O的切线,∴OP⊥AP,OQ⊥BQ,∴∠APO=∠BQO=90°,在Rt△APO和Rt△BQO中,∵OA=OB,OP=OQ,∴Rt△APO≌Rt△BQO,∴AP=BQ;
(2)∵Rt△APO≌Rt△BQO,∴∠AOP=∠BOQ,∴P、O、Q三点共线,∵在Rt△BOQ中,cosB=![]() ,∴∠B=30°,∠BOQ=60°,∴OQ=
,∴∠B=30°,∠BOQ=60°,∴OQ=![]() OB=4,∵∠COD=90°,∴∠QOD=90°+60°=150°,∴优弧
OB=4,∵∠COD=90°,∴∠QOD=90°+60°=150°,∴优弧![]() 的长=
的长=![]() =
=![]() ;
;
(3)∵△APO的外心是OA的中点,OA=8,∴△APO的外心在扇形COD的内部时,OC的取值范围为4<OC<8.

 名校课堂系列答案
名校课堂系列答案【题目】有这样一个问题:探究函数![]() 的图象与性质.小东根据学习函数的经验,对函数
的图象与性质.小东根据学习函数的经验,对函数![]() 的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
的图象与性质进行了探究.下面是小东的探究过程,请补充完整:
(1)函数![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
(2)下表是x与y的几组对应值.
| ... |
|
|
|
|
|
|
| 1 | 2 | 3 | ... |
| ... |
|
|
|
|
|
|
|
|
| m | ... |
求m的值;
(3)如图,在平面直角坐标系中,已描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;

(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,![]() ).结合函数的图象,写出该函数的其它性质(写两条即可).
).结合函数的图象,写出该函数的其它性质(写两条即可).