题目内容
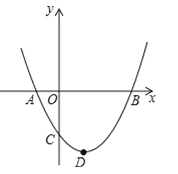
【题目】如图,二次函数![]() (a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( )
(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1和3,则下列结论正确的是( )
A.2a﹣b=0
B.a+b+c>0
C.3a﹣c=0
D.当a=![]() 时,△ABD是等腰直角三角形
时,△ABD是等腰直角三角形
【答案】D.
【解析】
试题分析:∵抛物线与x轴的交点A、B的横坐标分别为﹣1,3,∴抛物线的对称轴为直线x=1,则![]() =1,∴2a+b=0,∴选项A错误;
=1,∴2a+b=0,∴选项A错误;
∴当自变量取1时,对应的函数图象在x轴下方,∴x=1时,y<0,则a+b+c<0,∴选项B错误;
∵A点坐标为(﹣1,0),∴a﹣b+c=0,而b=﹣2a,∴a+2a+c=0,∴3a+c=0,∴选项C错误;
当a=![]() ,则b=﹣1,c=
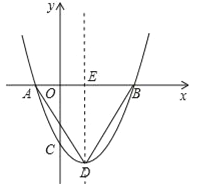
,则b=﹣1,c=![]() ,对称轴x=1与x轴的交点为E,如图,∴抛物线的解析式为
,对称轴x=1与x轴的交点为E,如图,∴抛物线的解析式为![]() ,把x=1代入得y=
,把x=1代入得y=![]() =﹣2,∴D点坐标为(1,﹣2),∴AE=2,BE=2,DE=2,∴△ADE和△BDE都为等腰直角三角形,∴△ADB为等腰直角三角形,∴选项D正确.
=﹣2,∴D点坐标为(1,﹣2),∴AE=2,BE=2,DE=2,∴△ADE和△BDE都为等腰直角三角形,∴△ADB为等腰直角三角形,∴选项D正确.
故选D.

练习册系列答案
相关题目