Question

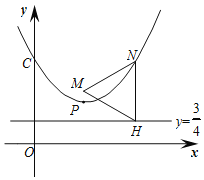
【题目】如图，抛物线的顶点P（m，1）（m＞0），与y轴的交点C（0，m2+1）．

（1）求抛物线的解析式（用含m的式子表示）

（2）点N（x，y）在该抛物线上，NH⊥直线y＝于点H，点M（m，）且∠NMH＝60°．

①求证：△MNH是等边三角形；

②当点O、P、N在同一直线上时，求m的值．

Answer 1

【答案】（1）该抛物线解析式是：y＝（x﹣m）2+1；（2）①证明见解析；②联立方程组，解得m＝．

【解析】

（1）设抛物线解析式把点C的坐标代入即可求得a的值；

（2）①证明NM＝NH即可；

②求点M、N的纵坐标的数量关系，得到点N的纵坐标；再求直线OP的解析式，求m的值．

解：（1）设抛物线解析式是y＝a（x﹣m）2+1（a≠0），

将C（0，m2+1）代入，得a（0﹣m）2+1＝m2+1

解得a＝1．

故该抛物线解析式是：y＝（x﹣m）2+1；

（2）①根据题意知，NH＝y﹣．

NM＝＝＝＝y﹣．

则NM＝NH．

又因为∠NMH＝60°，

所以△MNH是等边三角形；

②由①知，△MNH是等边三角形．则yM＝yN，即＝y．故yN＝ ．

由于点N（x，）在抛物线y＝（x﹣m）2+1上，

∴（x﹣m）2+1＝①

所以点N的坐标是（x，（x﹣m）2+1）．

设直线OP的解析式是y＝kx（k≠0）．

把P（m，1）（m＞0）代入，得mk＝1．

解得k＝．

故该直线方程是y＝．

把N（x，（x﹣m）2+1）代入，得（x﹣m）2+1＝②．

②联立方程组，解得m＝．