Question

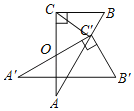
【题目】如图，在Rt△ABC中，∠C＝90°，∠A＝30°，AC＝8，O是AC的中点，把Rt△ABC绕着点O旋转得到Rt△A'B'C'，使得点C的对应点C'恰好落在AB上，则C，C'两点间的距离是_____．

Answer 1

【答案】4

【解析】

由旋转可知AC＝A'C'，AO＝CO，A'O＝C'O，再证明四边形AC'CA'是矩形，可得∠CC'A＝90°，由直角三角形的性质可求解．

解：如图，连接A'A，A'C，

∵O是AC的中点，

∴OC＝AO，

由旋转可知AC＝A'C'，AO＝CO，A'O＝C'O，

∴四边形AC'CA'是平行四边形

∵AC＝A'C'，

∴四边形AC'CA'是矩形，

∴∠CC'A＝90°，且∠CAB＝30°，AC＝8，

∴CC'＝4，

故答案为：4．