题目内容
如图,在△ABC中,AB=10,BC=21,sinB=| 4 | 5 |
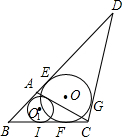 D分别相切于点E、F、G,且点E在线段AD上.
D分别相切于点E、F、G,且点E在线段AD上.(1)求△ABC的内切圆⊙Ol半径r;
(2)设⊙O的半径为x,CF的长为y,求y与x之间的函数解析式,并写出自变量x的取值范围;
(3)△DBC的面积值能否是周长值的两倍?如果能够,请求出BE的长;如果不能,请说明理由.
分析:(1)可作AH⊥BC于H,由三角形的面积入手,即可求解半径的长;
(2)要找y与x之间的函数解析式,可由△O1BI∽△OBF得出对应边成比例,而对于x的取值范围,则应保证其小于圆的半径;
(3)可先假设题中结论成立,通过面积的关系代入计算,得出x的值不满足题意,即得出结论不成立.
(2)要找y与x之间的函数解析式,可由△O1BI∽△OBF得出对应边成比例,而对于x的取值范围,则应保证其小于圆的半径;
(3)可先假设题中结论成立,通过面积的关系代入计算,得出x的值不满足题意,即得出结论不成立.
解答: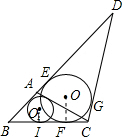 解:(1)作AH⊥BC于H,则AH=8,BH=6,CH=15,AC=17,
解:(1)作AH⊥BC于H,则AH=8,BH=6,CH=15,AC=17,
由S△ABC=
BC•AH=
(AB+BC+AC)r,
即
×21×8=
(10+21+17)r,
解得r=
.
(2)连接OB、OF、O1I,(I为⊙Ol与BC的切点),
BI=
(AB+BC-AC)=7,BF=21-y,
由△O1BI∽△OBF得
=
,
=
,
∴y与x之间的函数解析式为y=-2x+21.
当BD∥CD时,两平行线之间距离为BC×sinB=
,此时⊙O的半径为
,BF=21-y=2x=BE≥BA,x≥5,
∴函数自变量x的取值范围为5≤x<
.
(3)假设能够,则S△DBC=
(BD+BC+CD)x,S△DBC=
•
S△DBC•x,x=4.
这不符合题意,
所以△DBC的面积值不可能是周长值的两倍.
 解:(1)作AH⊥BC于H,则AH=8,BH=6,CH=15,AC=17,
解:(1)作AH⊥BC于H,则AH=8,BH=6,CH=15,AC=17,由S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
即
| 1 |
| 2 |
| 1 |
| 2 |
解得r=
| 7 |
| 2 |
(2)连接OB、OF、O1I,(I为⊙Ol与BC的切点),
BI=
| 1 |
| 2 |
由△O1BI∽△OBF得
| O 1I |
| BI |
| OF |
| BF |
| ||
| 7 |
| x |
| 21-y |
∴y与x之间的函数解析式为y=-2x+21.
当BD∥CD时,两平行线之间距离为BC×sinB=
| 84 |
| 5 |
| 42 |
| 5 |
∴函数自变量x的取值范围为5≤x<
| 42 |
| 5 |
(3)假设能够,则S△DBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
这不符合题意,
所以△DBC的面积值不可能是周长值的两倍.
点评:本题主要考查了相似三角形的判定及性质以及三角形的面积计算和圆形切线的性质,圆形与三角形结合,题目有一定的难度,解题时应多思考.

练习册系列答案
相关题目
 20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B=
20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B= 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为 2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( )
2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( ) 如图,在△ABC中,AB=AC,且∠A=100°,∠B=
如图,在△ABC中,AB=AC,且∠A=100°,∠B=