题目内容
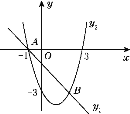
【题目】已知y=x2+bx+c的图象向右平移2个单位长度,再向下平移3个单位长度,得到的图象对应的函数表达式为y=x2-2x-3.
(1) 求b,c;
(2)求原函数图象的顶点坐标;
(3)求两个图象顶点之间的距离.
【答案】(1)2;0;(2)顶点坐标为(-1,-1);(3)原两个顶点之间的距离为![]() .
.
【解析】
先把平移后的函数化为顶点式表达,再根据二次函数的平移变化得出b、c的值,即可求出相应的顶点坐标即两顶点之间的距离.
(1)2;0
∵y=x2-2x-3= (x-1)2-4,
此函数经过向右平移2个单位长度,再向下平移3个单位长度得到,
故平移前的函数为y= (x+1)2-1,
y= (x+1)2-1=y=x2+2x,
故a=1,b=2;
(2)原函数的表达式为y= (x+1)2-1.
∴其图象的顶点坐标为(-1,-1).
(3)原图象的顶点为(-1,-1),新图象的顶点为(1,-4).
由勾股定理易得两个顶点之间的距离为![]() .
.

练习册系列答案
相关题目