题目内容
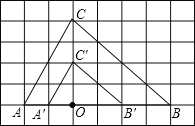
【题目】如图，在6×8的网格图中，每个小正方形边长均为1，点O和△ABC的顶点均为小正方形的顶点．
（1）以O为位似中心，在网格图中作△A′B′C′，使△A′B′C′和△ABC位似，且位似比为1：2．
（2）连接（1）中的AA′，求四边形AA′C′C的周长．（结果保留根号）
【答案】（1）见解析；（2）3+3
．
【解析】
试题分析：（1）取OA的中点A′，OB的中点B′，OC的中点C′，然后顺次连接即可；
（2）根据勾股定理列式求出AC、A′C′的长，再根据周长公式列式进行计算即可得解．
解：（1）如图所示，△A′B′C′即为所求作的三角形；
（2）根据勾股定理，AC=
=2，
A′C′=
=，
所以，四边形AA′C′C的周长为：1++2+2=3+3．
练习册系列答案
相关题目
