Question

在△ABC中，若AB=AC，中线AD=

3

，cosB=

3

2

，则△ABC的周长为（　　）

• A．4+6

  3

• B．6+4

  3

• C．6+6

  3

• D．以上都不对

Answer 1

分析：根据等腰三角形的性质得出AD⊥BC，进而得出∠B=30°，再利用锐角三角函数关系求出BD的长，进而得出BC的长，即可得出答案．

解答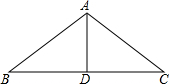：解：∵AB=AC，中线AD=

3

，
∴AD⊥BC，
∵cosB=

3

2

，
∴∠B=30°，
∴AB=2AD=2

3

，
∴BD=2

3

×cos30°=3，
∴BC=3×2=6，AB=AC=2

3

，
∴△ABC的周长为：6+2

3

+2

3

=6+4

3

．
故选：B．

点评：此题主要考查了解直角三角形和等腰三角形的性质等知识，根据已知得出AB的长是解题关键．