题目内容

如图．用长为18cm的篱笆（虚线部分），两面靠墙围成矩形的苗圃，设矩形的一边长为x（m），面y（m2），当x=______时，所围苗圃面积最大．
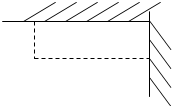
设苗圃的一边长为xm，则矩形的另一边长为（18-x）m，
则y=x（18-x）=-x2+18x
∵y=-x2+18x=-（x-9）2+81
∴当x=9时，苗圃的面积最大，最大面积是81m2．
故答案为：9．
练习册系列答案
相关题目
对于二次函数y=ax2+bx+c（a≠0），我们把使函数值为0的实数x叫做这个函数的零点．若二次函数y=-x2+2x+m的部分图象如图所示，则其零点为______．
如图，抛物线y=
1
2
x2+mx+n与x轴交于A、B两点，与y轴交于C点，四边形OBHC为矩形，CH的延长线交抛物线于点D（5，2），连接BC、AD．
（1）求C点的坐标及抛物线的解析式；
（2）将△BCH绕点B按顺时针旋转90°后再沿x轴对折得到△BEF（点C与点E对应），判断点E是否落在抛物线上，并说明理由；
（3）设过点E的直线交AB边于点P，交CD边于点Q．问是否存在点P，使直线PQ分梯形ABCD的面积为1：3两部分？若存在，求出P点坐标；若不存在，请说明理由．
如图，抛物线y=
3
8
x2-
3
4
x+c分别交x轴的负半轴和正半轴于点A（x1，0）、B（x2，0），交y轴的负轴于点C，且tan∠OAC=2tan∠OBC，动点P从点A出发向终点B运动，同时动点Q从点B出发向终点C运动，P、Q的运动速度均为每秒1个单位长度，且当其中有一个点到达终点时，另一个点也随之停止运动，设运动的时间是t秒．

（1）试说明OB=2OA；
（2）求抛物线的解析式；
（3）当t为何值时，△PBQ是直角三角形？
（4）当t为何值时，△PBQ是等腰三角形？
用总长为40m的篱笆围成一个矩形花圃，花圃的最大面积是______．
二次函数y=ax2+4x+a的最大值是3，则a的值是______．
如图，在平面直角坐标系中，矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上，OA=4，OC=2．点P从点O出发，沿x轴以每秒1个单位长的速度向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒．将线段CP的中点绕点P按顺时针方向旋转90°得点D，点D随点P的运动而运动，连接DP、DA．
（1）请用含t的代数式表示出点D的坐标；
（2）求t为何值时，△DPA的面积最大，最大为多少？
（3）在点P从O向A运动的过程中，△DPA能否成为直角三角形？若能，求t的值．若不能，请说明理由；
（4）请直接写出随着点P的运动，点D运动路线的长．
3
16
可表示成不同的随机事件发生的概率，请你设计一种实验，使某种事件发生的概率是
3
16
．列出图表表示．
企业的污水处理有两种方式，一种是输送到污水厂进行集中处理，另一种是通过企业的自身设备进行处理．某企业去年每月的污水量均为12000吨，由于污水厂处于调试阶段，污水处理能力有限，该企业投资自建设备处理污水，两种处理方式同时进行．1至6月，该企业向污水厂输送的污水量y1（吨）与月份x（1≤x≤6，且x取整数）之间满足的函数关系如下表：
月份x（月）123456
输送的污水量y1（吨）1200060004000300024002000
7至12月，该企业自身处理的污水量y2（吨）与月份x（7≤x≤12，且x取整数）之间满足二次函数关系式为y2=ax2+c(a≠0)．其图象如图所示．1至6月，污水厂处理每吨污水的费用：z1（元）与月份x之间满足函数关系式：z1=
1
2
x，该企业自身处理每吨污水的费用：z2（元）与月份x之间满足函数关系式：z2=
3
4
x-
1
12
x2；7至12月，污水厂处理每吨污水的费用均为2元，该企业自身处理每吨污水的费用均为1.5元．
（1）请观察题中的表格和图象，用所学过的一次函数、反比例函数或二次函数的有关知识，分别直接写出y1，y2与x之间的函数关系式；
（2）请你求出该企业去年哪个月用于污水处理的费用W（元）最多，并求出这个最多费用；
（3）今年以来，由于自建污水处理设备的全面运行，该企业决定扩大产能并将所有污水全部自身处理，估计扩大产能后今年每月的污水量都将在去年每月的基础上增加a%，同时每吨污水处理的费用将在去年12月份的基础上增加（a-30）%，为鼓励节能降耗，减轻企业负担，财政对企业处理污水的费用进行50%的补助．若该企业每月的污水处理费用为18000元，请计算出a的整数值．
（参考数据：
231
≈15.2，
419
≈20.5，
809
≈28.4）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网