题目内容
24、如图,a、b两数在数轴上对应点的位置如图所示:

(1)在数轴上标出-a、-b对应的点,并将a、b、-a、-b用“<”连接起来;
(2)化简:|2(-a+1)|-|b-2|+2|a-b|;
(3)x是数轴上的一个数,试讨论:x为有理数时,|x+1|+|x-2|是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由.

(1)在数轴上标出-a、-b对应的点,并将a、b、-a、-b用“<”连接起来;
(2)化简:|2(-a+1)|-|b-2|+2|a-b|;
(3)x是数轴上的一个数,试讨论:x为有理数时,|x+1|+|x-2|是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由.
分析:(1)在数轴上标出-a、-b对应的点,比较直观的可以将a、b、-a、-b用“<”连接起来;
(2)读数轴得出a、b的取值,从而确定-a+1>0,b-2<0,a-b<0,根据绝对值的定义可求解;
(3)可分类讨论:当x<-1,-1≤x≤2,x>2时,化简原式取最小值.
(2)读数轴得出a、b的取值,从而确定-a+1>0,b-2<0,a-b<0,根据绝对值的定义可求解;
(3)可分类讨论:当x<-1,-1≤x≤2,x>2时,化简原式取最小值.
解答:解:(1)
-b<a<-a<b;
(2)∵-a+1>0,b-2<0,a-b<0,
∴|2(-a+1)|-|b-2|+2|a-b|,
=2(-a+1)-[-(b-2)]+2[-(a-b)],
=-4a+3b;
(3)|x+1|+|x-2|存在最小值,最小值为3.
当x<-1时,|x+1|+|x-2|=-x-1-x+2=-2x+1;
当-1≤x≤2时,|x+1|+|x-2|=x+1-x+2=3;
当x>2时,|x+1|+|x-2|=x+1+x-2=2x-1;
∴|x+1|+|x-2|存在最小值,最小值为3.

-b<a<-a<b;
(2)∵-a+1>0,b-2<0,a-b<0,
∴|2(-a+1)|-|b-2|+2|a-b|,
=2(-a+1)-[-(b-2)]+2[-(a-b)],
=-4a+3b;
(3)|x+1|+|x-2|存在最小值,最小值为3.
当x<-1时,|x+1|+|x-2|=-x-1-x+2=-2x+1;
当-1≤x≤2时,|x+1|+|x-2|=x+1-x+2=3;
当x>2时,|x+1|+|x-2|=x+1+x-2=2x-1;
∴|x+1|+|x-2|存在最小值,最小值为3.
点评:此题综合考查了数轴、绝对值的有关内容,用几何方法借助数轴来求解,非常直观,且不容易遗漏,体现了数形结合的优点.

练习册系列答案
相关题目
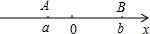 (1997•西宁)如图,a、b两数在数轴上的对应点为A、B,化简
(1997•西宁)如图,a、b两数在数轴上的对应点为A、B,化简