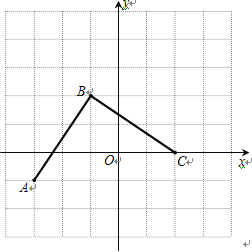��Ŀ����
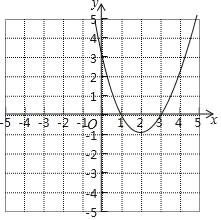
����Ŀ����ͼ����֪������y=ax2+bx��3����A����1��0����B��3��0������M��NΪ�������ϵĶ��㣬����M��MD��y�ᣬ��ֱ��BC�ڵ�D����x���ڵ�E������N��NF��x�ᣬ����Ϊ��F
(1)����κ���y=ax2+bx��3�ı���ʽ��
(2)��M�����������϶Գ����Ҳ�ĵ㣬���ı���MNFEΪ�����Σ���������ε������
(3)��M�����������϶Գ������ĵ㣬�ҡ�DMN=90�㣬MD=MN����ֱ��д����M�ĺ����꣮
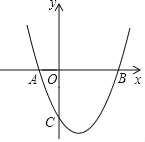
���𰸡�(1) y=x2��2x��3�� (2) �����ε����Ϊ24+8![]() ��24��8
��24��8![]() �� (3) ��M�ĺ�����Ϊ��1��
�� (3) ��M�ĺ�����Ϊ��1��![]() ��
��
��������
��1����A����1��0����B��3��0��������������y=ax2+bx��3�����ô���ϵ����������ö��κ���y=ax2+bx��3�ı���ʽ����2�����M������Ϊ��m��m2��2m��3������m��1���ֱ��ʾ��ME=|��m2+2m��3|��MN=2m��2�����ı���MNFEΪ������֪ME=MN���ݴ��г����̣������������ɵ�m��ֵ��������������ε��������3�������ô���ϵ�������ֱ��BC�Ľ���ʽ�����M������Ϊ��t��t2��2t��3������t��1�����N��2��t��t2��2t��3������D��t��t��3������MD=MN�г����̣����ݵ�M��λ�÷����������ɵã�
(1)��A����1��0����B��3��0������y=ax2+bx��3��
�ã�![]() ��
��
���![]() ��
��
�ʸ������߽���ʽΪ��y=x2��2x��3��
(2)��(1)֪�������߽���ʽΪ��y=x2��2x��3=��x��1��2��4��
��������ߵĶԳ�����x=1����������Ϊ��1����4����
��ͼ�����M����Ϊ��m��m2��2m��3��������m��1��
��ME=|��m2+2m+3|��
��M��N����x=1�Գƣ��ҵ�M�ڶԳ����Ҳ࣬
���N�ĺ�����Ϊ2��m��
��MN=2m��2��
���ı���MNFEΪ�����Σ�
��ME=MN��
��|��m2+2m+3|=2m��2��
�����������
�ٵ���m2+2m+3=2m��2ʱ����ã�m1=![]() ��m2=��
��m2=��![]() �����������⣬��ȥ����
�����������⣬��ȥ����
��m=![]() ʱ�������ε����Ϊ��2
ʱ�������ε����Ϊ��2![]() ��2��2=24��8
��2��2=24��8![]() ��
��
�ڵ���m2+2m+3=2��2mʱ����ã�m3=2+![]() ��m4=2��
��m4=2��![]() �����������⣬��ȥ����
�����������⣬��ȥ����
��m=2+![]() ʱ�������ε����Ϊ[2��2+
ʱ�������ε����Ϊ[2��2+![]() ����2]2=24+8
����2]2=24+8![]() ��
��
���������������ε����Ϊ24+8![]() ��24��8
��24��8![]() ��
��
(3)��BC����ֱ�߽���ʽΪy=px+q��
�ѵ�B��3��0����C��0����3���������ʽ��
�ã�![]() ����ã�
����ã�![]() ��
��
��ֱ��BC�ĺ�������ʽΪy=x��3��
���M��������t��t2��2t��3��������t��1��
���N��2��t��t2��2t��3������D��t��t��3����
��MN=2��t��t=2��2t��MD=|t2��2t��3��t+3|=|t2��3t|��
��MD=MN��
��|t2��3t|=2��2t��
�����������
�ٵ�t2��3t=2��2tʱ�����t1=��1��t2=2�����������⣬��ȥ����
�ڵ�3t��t2=2��2tʱ�����t3=![]() ��t2=
��t2=![]() �����������⣬��ȥ����
�����������⣬��ȥ����
������������M�ĺ�����Ϊ��1��![]() ��
��