题目内容
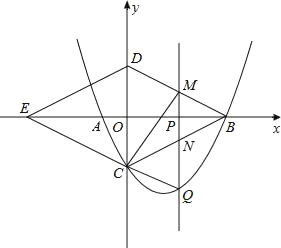
【题目】如图,已知函数![]() 的图象为直线
的图象为直线![]() ,函数
,函数![]() 的图象为直线
的图象为直线![]() ,直线
,直线![]() 、
、![]() 分别交
分别交![]() 轴于点
轴于点![]() 和点
和点![]() ,分别交
,分别交![]() 轴于点
轴于点![]() 和
和![]() ,
,![]() 和
和![]() 相交于点
相交于点![]()
(1)填空:![]() ;求直线
;求直线![]() 的解析式为 ;
的解析式为 ;
(2)若点![]() 是
是![]() 轴上一点,连接
轴上一点,连接![]() ,当
,当![]() 的面积是
的面积是![]() 面积的2倍时,请求出符合条件的点
面积的2倍时,请求出符合条件的点![]() 的坐标;
的坐标;
(3)若函数![]() 的图象是直线
的图象是直线![]() ,且
,且![]() 、
、![]() 、
、![]() 不能围成三角形,直接写出
不能围成三角形,直接写出![]() 的值.
的值.

【答案】(1)![]() ,直线
,直线![]() 的解析式为
的解析式为![]() ;(2)
;(2)![]() 点的坐标为
点的坐标为![]() 或
或![]() ;(3)
;(3)![]() 的值为
的值为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)将点![]() 坐标代入
坐标代入![]() 中,即可得出结论;将点
中,即可得出结论;将点![]() ,
,![]() 坐标代入
坐标代入![]() 中,即可得出结论;
中,即可得出结论;
(2)先利用两三角形面积关系判断出![]() ,再分两种情况,即可得出结论;
,再分两种情况,即可得出结论;
(3)分三种情况,利用两直线平行,![]() 相等或经过点
相等或经过点![]() 讨论即可得出结论.
讨论即可得出结论.
解:(1)![]() 点
点![]() 在函数
在函数![]() 的图象上,
的图象上,
![]() ,
,
![]() ,
,
![]() 直线
直线![]() 过点
过点![]() 、
、![]() ,
,
可得方程组为![]() ,
,
解得![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ;
;
故答案为:![]() ;
;![]()
(2)![]() 是
是![]() 与
与![]() 轴的交点,当
轴的交点,当![]() 时,
时,![]() ,
,
![]() ,
,![]() 坐标为
坐标为![]() ,
,
又![]() 的面积是
的面积是![]() 面积的2倍,
面积的2倍,
![]()
第一种情况,当![]() 在线段
在线段![]() 上时,
上时,
![]() ,
,
![]() ,即
,即![]() ,
,
∴![]() ,
,
![]() 坐标
坐标![]() ,
,
第二种情况,当![]() 在射线
在射线![]() 上时,
上时,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 坐标
坐标![]() ,
,
![]() 点的坐标为
点的坐标为![]() 或
或![]() ;
;
(3)![]() 、
、![]() 、
、![]() 不能围成三角形,
不能围成三角形,
![]() 直线
直线![]() 经过点
经过点![]() 或
或![]() 或
或![]() ,
,
①![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入到解析式中得:
代入到解析式中得:
![]() ,
,
![]() ,
,
②当![]() 时,
时,
∵直线![]() 的解析式为
的解析式为![]() ,
,
![]() ,
,
③当![]() 时,
时,
∵直线![]() 的解析式为
的解析式为![]() ,
,
![]() ,
,
即![]() 的值为
的值为![]() 或
或![]() 或
或![]() .
.

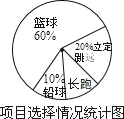
【题目】光明中学七年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼,每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.
项目选择情况统计图训练后篮球定时定点投篮测试进球数统计表
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
请你根据图表中的信息回答下列问题:
(1)选择长跑训练的人数占全班人数的百分比是_____%,该班共有同学_____人;
(2)求训练后篮球定时定点投篮人均进球数;
(3)根据测试资料,训练后篮球定时定点投篮的人均进球数比训练之前人均进球数增加25%.请求出参加训练之前的人均进球数.