题目内容
解下列不等式,并把解集在数轴上表示出来:
(1)3(x+2)-8≥1-2(x-1);
(2)x-
≤2-
.
(1)3(x+2)-8≥1-2(x-1);
(2)x-
| x-1 |
| 2 |
| x+2 |
| 3 |
分析:(1)根据解不等式的步骤,先去括号,再移项,系数化1即可得出答案,再根据求出不等式的解集,根据“大于向右,小于向左,包括端点用实心,不包括端点用空心”的原则将解集在数轴表示出来.
(2)先去分母,再去括号,然后合并同类项,系数化1即可得出答案,再在数轴上画出解集即可.
(2)先去分母,再去括号,然后合并同类项,系数化1即可得出答案,再在数轴上画出解集即可.
解答:解:(1)3(x+2)-8≥1-2(x-1),
3x+6-8≥1-2x+2,
3x+2x≥1+2-6+8,
5x≥5,
x≥1;
如图:
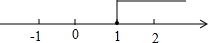
(2)x-
≤2-
,
6x-3(x-1)≤12-2(x+2),
6x-3x+3≤12-2x-4,
3x+2x≤8-3,
5x≤5,
x≤1.
如下:

3x+6-8≥1-2x+2,
3x+2x≥1+2-6+8,
5x≥5,
x≥1;
如图:

(2)x-
| x-1 |
| 2 |
| x+2 |
| 3 |
6x-3(x-1)≤12-2(x+2),
6x-3x+3≤12-2x-4,
3x+2x≤8-3,
5x≤5,
x≤1.
如下:

点评:此题考查了一元一次不等式的解和在数轴上表示不等式的解集,解不等式要依据不等式的基本性质:(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变进行解答.

练习册系列答案
相关题目
 (2012•北碚区模拟)解下列不等式,并把解集表示在数轴上:x-4≤
(2012•北碚区模拟)解下列不等式,并把解集表示在数轴上:x-4≤