题目内容
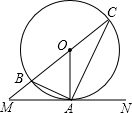如图，MN切⊙O于A点，AC为弦，BC为直径，那么下列命题中假命题是（ ）| A、∠MAB和∠ABC互余 | ||
| B、∠CAN=∠ABC | ||
C、OA=
| ||
| D、MA2=MB•BC |
分析：首先根据已知条件看能够证得什么条件，然后再判断各选项是否正确．
解答：解：∵BC是⊙O的直径，
∴∠BAC=90°，
∴∠MAB+∠CAN=90°；
∵MN切⊙O于A，
∴MA2=MB•MC，（故D错误）
∠CAN=∠CBA，（故B正确）
∴∠MAB+∠CBA=90°；（故A正确）
∵OA是⊙O的半径，BC是⊙O的直径，
∴BC=2OA；（故C正确）
故选D．
∴∠BAC=90°，
∴∠MAB+∠CAN=90°；
∵MN切⊙O于A，
∴MA2=MB•MC，（故D错误）
∠CAN=∠CBA，（故B正确）
∴∠MAB+∠CBA=90°；（故A正确）
∵OA是⊙O的半径，BC是⊙O的直径，
∴BC=2OA；（故C正确）
故选D．
点评：此题主要考查了圆周角定理、切线的性质以及切割线定理的应用．
练习册系列答案
英才点津系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
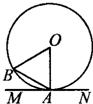16、如图，MN切⊙O于点A，∠AOB=60°，那么∠BAM等于（ ）
（2004•呼和浩特）如图，MN切⊙O于P，AB是⊙O的弦，AM⊥MN于M，BN⊥MN于N，PQ⊥AB于Q．
如图，MN切⊙O于A点，AC为弦，BC为直径，∠CAN=65°，则∠BMA的度数为