题目内容
已知两个样本,甲:2,4,6,8,10;乙:1,3,5,7,9,用
与
分别表示这两个样本的方差,则下列结论:其中正确的结论是
①
>
,②
<
,③
=
.
| S | 2 甲 |
| S | 2 乙 |
③
③
(填序号).①
| S | 2 甲 |
| S | 2 乙 |
| S | 2 甲 |
| S | 2 乙 |
| S | 2 甲 |
| S | 2 乙 |
分析:先分别求出甲和乙的平均数,再根据方差公式S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2]进行计算即可.
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
解答:解:甲的平均数是:(2+4+6+8+10)÷5=6,
乙的平均数是(1+3+5+7+9)÷5=5,
=
[(2-6)2+(4-6)2+(6-6)2+(8-6)2+(10-6)2]=8,
=
[(1-5)2+(3-5)2+(5-5)2+(7-5)2+(9-5)2]=8,
则
=
;
故选③.
乙的平均数是(1+3+5+7+9)÷5=5,
| S | 2 甲 |
| 1 |
| 5 |
| S | 2 乙 |
| 1 |
| 5 |
则
| S | 2 甲 |
| S | 2 乙 |
故选③.
点评:此题考查了方差,一般地设n个数据,x1,x2,…xn的平均数为
,则方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |

练习册系列答案
相关题目
 与s
与s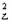 分别表示这两个样本的方差,则下列结论:①s
分别表示这两个样本的方差,则下列结论:①s >s
>s ;②s
;②s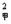 <s
<s ;③s
;③s =s
=s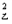 ,其中正确的结论是( )(填写序号)。
,其中正确的结论是( )(填写序号)。