题目内容
 如图,D,E是等边△ABC两边上的两个点,且AE=CD,连接BE,与AD交于点P,过点B作BQ⊥AD于Q,那么BP:PQ=
如图,D,E是等边△ABC两边上的两个点,且AE=CD,连接BE,与AD交于点P,过点B作BQ⊥AD于Q,那么BP:PQ=分析:易证△ABE≌△CAD,即可求得∠CAD=∠ABE,进而可以求得∠BPQ=60°,根据特殊角的三角函数值即可求得BP:PQ的值,即可解题.
解答:解:在△ABE和△CAD中,
,
∴△ABE≌△CAD,(SAS)
∴∠CAD=∠ABE,
∵∠CAD+∠PAB=60°,
∴∠BPQ=∠BAP+∠ABE=∠CAD+∠PAB=60°,
∴在直角△BPQ中,PQ:BP=sin30°=1:2,
∴BP:PQ=2:1.
故答案为 2:1.
|
∴△ABE≌△CAD,(SAS)
∴∠CAD=∠ABE,
∵∠CAD+∠PAB=60°,
∴∠BPQ=∠BAP+∠ABE=∠CAD+∠PAB=60°,
∴在直角△BPQ中,PQ:BP=sin30°=1:2,
∴BP:PQ=2:1.
故答案为 2:1.
点评:本题考查了全等三角形的判定和全等三角形对应角相等的性质,特殊角的三角函数值,三角函数在直角三角形中的运用,本题中求∠BPQ=60°是解题的关键.

练习册系列答案
相关题目
 29、如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.
29、如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.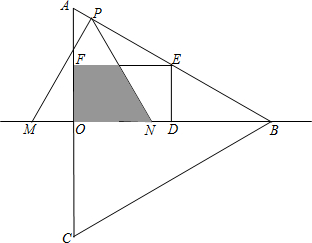 边在△AOB内部作如图所示的矩形ODEF,点E在线段AB上.
边在△AOB内部作如图所示的矩形ODEF,点E在线段AB上. 如图,D、E是等边△ABC的BC边和AC边上的点,BD=CE,AD与BE相交于P点,则∠APE的度数是( )
如图,D、E是等边△ABC的BC边和AC边上的点,BD=CE,AD与BE相交于P点,则∠APE的度数是( )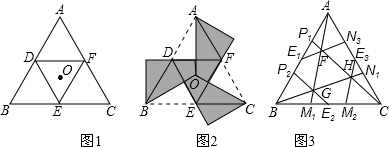
 如图所示,△ABC是等边三角形,D点是AC的中点,延长BC到E,使CE=CD,过D点作DM⊥BE,垂足是M
如图所示,△ABC是等边三角形,D点是AC的中点,延长BC到E,使CE=CD,过D点作DM⊥BE,垂足是M