题目内容
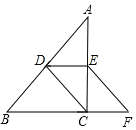
【题目】如图1,在正方形ABCD中,点E、F分别是边BC、CD上的点,且CE=CF,连接AE,AF,取AE的中点M,EF的中点N,连接BM,MN.
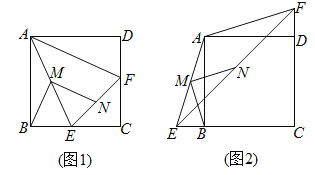
(1)请判断线段BM与MN的数量关系和位置关系,并予以证明.
(2)如图2,若点E在CB的延长线上,点F在CD的延长线上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
【答案】(1)BM=MN,BM⊥MN,证明见解析;(2)仍然成立,证明见解析
【解析】
(1)根据已知正方形ABCD的边角相等关系,推出△ABE≌△ADF(SAS),得出AE=AF,利用MN是△AEF的中位线,BM为Rt△ABE的中线,可得BM=MN,由外角性质,得出∠BME=∠1+∠3,再由MN∥AF,∠1+∠2+∠EAF=∠BAD=90°,等角代换可推出结论;
(2)同(1)思路一样,证明△ABE≌△ADF(SAS),利用外角性质和中位线平行关系,通过等角代换即得证明结论.
(1)BM=MN,BM⊥MN.
证明:在正方形ABCD中,∠BAD=∠ABC=∠ADC=90°,AB=AD=BC=DC,
∵CE=CF,
∴BC-CE=DC-CF,
∴BE=DF,
∴△ABE≌△ADF(SAS),
∴∠1=∠2,AE=AF,
∵M为AE的中点,N为EF的中点,
∴MN是△AEF的中位线,BM为Rt△ABE的中线.
∴MN∥AF,MN=![]() AF,BM=
AF,BM=![]() AE=AM,
AE=AM,
∴BM=MN,∠EMN=∠EAF,
∵BM=AM,
∴∠1=∠3, ∠2=∠3,
∴∠BME=∠1+∠3=∠1+∠2,
∴∠BMN=∠BME+∠EMN=∠1+∠2+∠EAF=∠BAD=90°,
∴BM⊥MN.
故答案为:BM=MN,BM⊥MN.
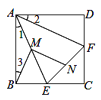
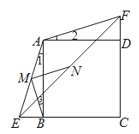
(2)(1)中结论仍然成立.
证明:在正方形ABCD中,∠BAD=∠ABC=∠ADC=90°,AB=AD=BC=DC,
∴∠ABE=∠ADF=90°,
∵CE=CF,∴CE-BC=CF-DC,∴BE=DF,
∴△ABE≌△ADF(SAS),∴∠1=∠2,AE=AF,
同理(1)得MN∥AF,MN=![]() AF,BM=
AF,BM=![]() AE=AM,
AE=AM,
∴BM=MN,
同理(1)得∠BME=∠1+∠2,∠EMN=∠EAF,
∴∠BMN=∠EMN-∠BME=∠EAF-(∠1+∠2)=∠BAD=90°,
∴BM⊥MN,
故答案为:结论仍成立.

【题目】甲、乙两人参加射击比赛,两人成绩如图所示.
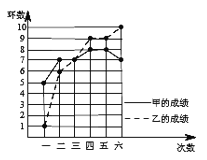
(1)填表:
平均数 | 方差 | 中位数 | 众数 | |
甲 | 7 | 1 | 7 | |
乙 | 9 |
(2)只看平均数和方差,成绩更好的是 .(填“甲”或“乙”)
(3)仅就折线图上两人射击命中环数的走势看,更有潜力的是 .(填“甲”或“乙”)