题目内容
【题目】如图，在平行四边形ABCD中，E为BC的中点，连接AE并延长交DC的延长线于点F．
(1)求证：AB=CF；
(2)当BC与AF满足什么数量关系时，四边形ABFC是矩形，并说明理由．
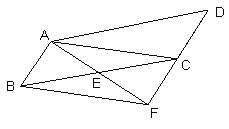
【答案】(1)见解析；(2)当BC=AF时，四边形ABFC是矩形，理由见解析
【解析】
（1）根据平行四边形的性质得到两角一边对应相等，利用AAS判定△ABE≌△FCE，从而得到AB=CF；
（2）由已知可得四边形ABFC是平行四边形，BC=AF，根据对角线相等的平行四边形是矩形，可得到四边形ABFC是矩形．
（1）证明：∵四边形ABCD是平行四边形
∴AB∥CD，AB=CD
∴
， 
∵E为BC的中点
∴BE=EC
∴ △ABE≌△FCE
∴ AB=CF.
(2)解:当BC=AF时,四边形ABFC是矩形.理由如下:
∵AB∥CF，AB=CF
∴四边形ABFC是平行四边形
∵BC=AF
∴四边形ABFC是矩形.
练习册系列答案
相关题目
【题目】甲、乙两位同学做抛骰子（均匀正方体形状）实验，他们共抛了60次，出现向上点数的次数如表：
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
（1）计算出现向上点数为6的频率．
（2）丙说：“如果抛600次，那么出现向上点数为6的次数一定是100次．”请判断丙的说法是否正确并说明理由．
（3）如果甲乙两同学各抛一枚骰子，求出现向上点数之和为3的倍数的概率．
