Question

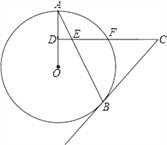
【题目】如图，AB是⊙O的弦，D为OA半径的中点，过D作CD⊥OA交弦AB于点E，交⊙O于点F，且CE=CB．

（1）求证：BC是⊙O的切线；

（2）连接AF，BF，求∠ABF的度数；

（3）如果CD=15，BE=10，sinA=，求⊙O的半径．

Answer 1

【答案】（1）证明见解析；

（2）∠ABF的度数为30°；

（3）⊙O的半径为.

【解析】试题分析：（1）连接OB，由圆的半径相等和已知条件证明∠OBC=90°，即可证明BC是 O的切线；（2）连接OF，AF，BF，首先证明△OAF是等边三角形，再利用圆周角定理：同弧所对的圆周角是所对圆心角的一半即可求出∠ABF的度数；（3）过点C作CG⊥BE于G，根据等腰三角形的性质得到EG=BE=5，由两角相等的三角形相似，△ADE∽△CGE，利用相似三角形对应角相等得到sin∠ECG=sinA=，在Rt△ECG中，利用勾股定理求出CG的长，根据三角形相似得到比例式，代入数据即可得到结果．

试题解析：(1)证明：连接OB

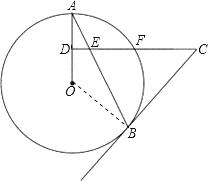
∵OB=OA，CE=CB，

∴∠A=∠OBA，∠CEB=∠ABC

又∵CD⊥OA

∴∠A+∠AED=∠A+∠CEB=90°

∴∠OBA+∠ABC=90°

∴OB⊥BC

∴BC是O的切线。

(2)连接OF，AF，BF，

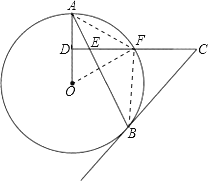
∵DA=DO，CD⊥OA，

∴AF=OF，

∵OA=OF，

∴△OAF是等边三角形，

∴∠AOF=60°

∴∠ABF=∠AOF=30°

(3)如图，过点C作CG⊥BE于G，

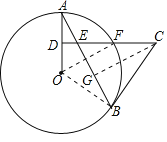
∵CE=CB，

∴EG=BE=5，

∵∠ADE=∠CGE=90°，∠AED=∠GEC，

∴∠GCE=∠A，

∴△ADE∽△CGE，

∴sin∠ECG=sinA=，即CE=13，

在Rt△ECG中，

∵CG=，

∵CD=15，CE=13，

∴DE=2，

∵△ADE∽△CGE，

∴，

∴AD=，CG=，

∴O的半径OA=2AD=.