题目内容
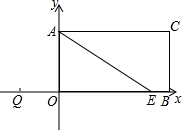 (2013•常州模拟)如图,矩形AOBC,A(0,3)、B(6,0),点E在OB上,∠AEO=30°,点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒.
(2013•常州模拟)如图,矩形AOBC,A(0,3)、B(6,0),点E在OB上,∠AEO=30°,点P从点Q(-4,0)出发,沿x轴向右以每秒1个单位长的速度运动,运动时间为t秒.(1)求点E的坐标;
(2)当∠PAE=15°时,求t的值;
(3)以点P为圆心,PA为半径的⊙P随点P的运动而变化,当⊙P与四边形AEBC的边(或边所在的直线)相切时,求t的值.
分析:(1)在Rt△AOE中求出OE,即可得出点E的坐标;
(2)如图1所示,当∠PAE=15°时,可得∠APO=45°,从而可求出AO=3,求出QP,即可得出t的值;
(3)以点P为圆心,PA为半径的⊙P与四边形AEBC的边(或边所在的直线)相切时,只有一种情况,也就是⊙P与AE边相切,且切点为点A,如图2所示,求出PE,得出QP,继而可得t的值.
(2)如图1所示,当∠PAE=15°时,可得∠APO=45°,从而可求出AO=3,求出QP,即可得出t的值;
(3)以点P为圆心,PA为半径的⊙P与四边形AEBC的边(或边所在的直线)相切时,只有一种情况,也就是⊙P与AE边相切,且切点为点A,如图2所示,求出PE,得出QP,继而可得t的值.
解答:解:(1)在Rt△AOE中,OA=3,∠AEO=30°,
∴OE=OAcot∠AEO=3
,
∴点E的坐标为(3
,0);
(2)如图1所示:
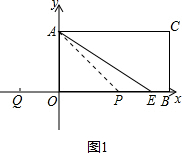
∵∠PAE=15°,∠AEO=30°,
∴∠APO=∠PAE+∠AEO=45°,
∴OP=OA=3,
∴QP=7,
∴t=7秒;
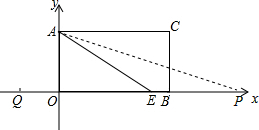
如图,∵∠AEO=30°,∠PAE=15°,
∴∠APE=15°=∠PAE,
∴AE=PE,
∵AE=
=6,
∴t=QP=OQ+OE+PE=10+3
;
∴t=7或10+3
s.
(3)∵PA是⊙P的半径,且⊙P与AE相切,
∴点A为切点,如图2所示:
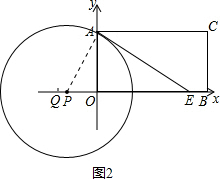
∵AE=6,∠AEO=30°,
∴PE=
=4
,
∴QP=QE-PE=(4+3
)-4
=4-
,
∴t=(4-
)秒.
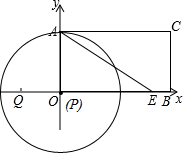
当点P与O重合时,⊙P与AC相切,
∴t=4秒;
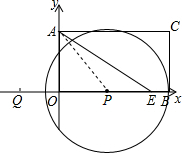
当PA=PB时,⊙P与BC相切,
设OP=x,则PB=PA=6-x,
在Rt△OAP中,x2+32=(6-x)2,
解得:x=
,
∴t=4+
=
(秒);
∴t=4-
或4或
秒.
∴OE=OAcot∠AEO=3
| 3 |
∴点E的坐标为(3
| 3 |
(2)如图1所示:

∵∠PAE=15°,∠AEO=30°,
∴∠APO=∠PAE+∠AEO=45°,
∴OP=OA=3,
∴QP=7,
∴t=7秒;

如图,∵∠AEO=30°,∠PAE=15°,
∴∠APE=15°=∠PAE,
∴AE=PE,
∵AE=
| AO |
| sin30° |
∴t=QP=OQ+OE+PE=10+3
| 3 |
∴t=7或10+3
| 3 |
(3)∵PA是⊙P的半径,且⊙P与AE相切,
∴点A为切点,如图2所示:

∵AE=6,∠AEO=30°,
∴PE=
| AE |
| cos∠AEO |
| 3 |
∴QP=QE-PE=(4+3
| 3 |
| 3 |
| 3 |
∴t=(4-
| 3 |

当点P与O重合时,⊙P与AC相切,
∴t=4秒;

当PA=PB时,⊙P与BC相切,
设OP=x,则PB=PA=6-x,
在Rt△OAP中,x2+32=(6-x)2,
解得:x=
| 9 |
| 4 |
∴t=4+
| 9 |
| 4 |
| 25 |
| 4 |
∴t=4-
| 3 |
| 25 |
| 4 |
点评:本题考查了圆的综合,涉及了圆与直线的位置关系、锐角三角函数的定义及外角的性质,难点在第三问,关键是判断出符合题意的情况,然后画出图形,难度较大.

练习册系列答案
相关题目
 (2013•常州模拟)如图,l1∥l2∥l3,且l1,l2之间的距离为2,l2,l3之间的距离为3.若点A,B,C分别在直线l1,l2,l3上,且AC⊥BC,AC=BC,则AB的长是
(2013•常州模拟)如图,l1∥l2∥l3,且l1,l2之间的距离为2,l2,l3之间的距离为3.若点A,B,C分别在直线l1,l2,l3上,且AC⊥BC,AC=BC,则AB的长是 (2013•常州模拟)如图,∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.当AC=3时,AD长是多少?(sin25°≈0.4226,结果精确到0.01)
(2013•常州模拟)如图,∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.当AC=3时,AD长是多少?(sin25°≈0.4226,结果精确到0.01)