题目内容
如图,等边△ABC在直角坐标系xOy中,已知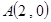 ,
,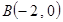 ,点C绕点A顺时针方向旋转120°得到点C1,点C1绕点B顺时针方向旋转120°得到C2,点C2绕点C顺时针方向旋转150°得到点C3,则点C3的坐标是
,点C绕点A顺时针方向旋转120°得到点C1,点C1绕点B顺时针方向旋转120°得到C2,点C2绕点C顺时针方向旋转150°得到点C3,则点C3的坐标是
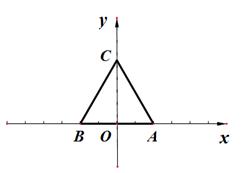
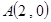 ,
,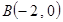 ,点C绕点A顺时针方向旋转120°得到点C1,点C1绕点B顺时针方向旋转120°得到C2,点C2绕点C顺时针方向旋转150°得到点C3,则点C3的坐标是
,点C绕点A顺时针方向旋转120°得到点C1,点C1绕点B顺时针方向旋转120°得到C2,点C2绕点C顺时针方向旋转150°得到点C3,则点C3的坐标是 
(0,12+2 ).
).
 ).
).试题分析:根据等边三角形的性质得到CA=CB=AB=4,∠CAB=∠CBA=∠BCA=60°,则∠BOC=30°,OC=
 OB=2
OB=2 ,再根据旋转的性质得到点C1在BA的延长线上,且AC1=4,点C2在CB的延长线上,且BC2=8,点C3在y轴的正半轴上,且CC3=12,然后写出点C3的坐标.
,再根据旋转的性质得到点C1在BA的延长线上,且AC1=4,点C2在CB的延长线上,且BC2=8,点C3在y轴的正半轴上,且CC3=12,然后写出点C3的坐标.试题解析:∵△ABC为等边三角形,
∴CA=CB=AB=4,∠CAB=∠CBA=∠BCA=60°,
∴∠BOC=30°,OC=
 OB=2
OB=2 ,
,∵点C绕点A顺时针方向旋转120°得到点C1,
∴点C1在BA的延长线上,且AC1=4,
∵点C1绕点B顺时针方向旋转120°得到C2,
∴点C2在CB的延长线上,且BC2=8,
∵点C2绕点C顺时针方向旋转150°得到点C3,
∴点C3在y轴的正半轴上,且CC3=12,
∴点C3的坐标是(0,12+2
 ).
).故答案为(0,12+2
 ).
).考点: 1.坐标与图形变化-旋转;2.等边三角形的性质.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目


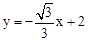 与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转60°后得到△AO'B',则点B'的坐标是
与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转60°后得到△AO'B',则点B'的坐标是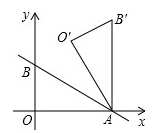
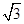 ,4) B.(4,2
,4) B.(4,2 在
在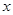 轴上,则点P的坐标为( )
轴上,则点P的坐标为( )

 是第二象限的点,则
是第二象限的点,则 的取值范围是 .
的取值范围是 .