题目内容
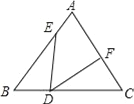
【题目】把一副三角板如图甲放置,其中![]() ,
, ![]() ,
, ![]() ,斜边
,斜边![]() ,
, ![]() ,把
,把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
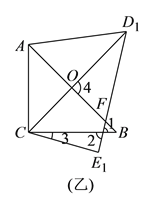
得到![]() (如图乙),这时
(如图乙),这时![]() 与
与![]() 相交于点
相交于点![]() ,与
,与![]() 相交于点
相交于点![]() .
.
(![]() )求
)求![]() 的度数.
的度数.
(![]() )求线段
)求线段![]() 的长.
的长.
(![]() )若把
)若把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,这时点
,这时点![]() 在
在![]() 的内部,外部,还是边上?证明你的判断.
的内部,外部,还是边上?证明你的判断.


【答案】(1) ![]() ;(2)5cm;(3) 点
;(2)5cm;(3) 点![]() 在
在![]() 内部,理由见解析
内部,理由见解析
【解析】试题分析:(1)如图乙,由三角形外角性质易得:∠AFE1=∠B+∠1,而∠1=∠2=180°-∠3-∠E1,而由已知条件可得:∠3=15°,∠E1=∠DEC=90°,∠B=45°,从而可求出∠AFE1,(也可以在四边形ACE1F中用四边形内角和来求);
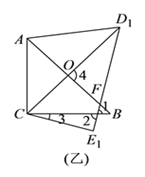
(2)由(1)中∠AFE1=120°,易得∠OFD1=60°,再由∠CD1E1=30°,可得∠4=90°,从而推得CD1⊥AB,又∵△ABC是等腰直角三角形,∴可得OA=OC=![]() AB=3(cm),∴OD1=CD1-OC=4(cm),最后在Rt△AOD1中由勾股定理可求得AD1;
AB=3(cm),∴OD1=CD1-OC=4(cm),最后在Rt△AOD1中由勾股定理可求得AD1;
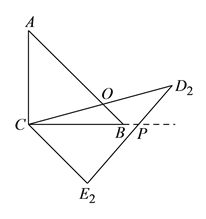
(3)如图,设CB(或CB的延长线)交E2D2于点P,由已知易得:CE2=![]() CD=
CD=![]() ,BC=
,BC=![]() ,证△CE2P是等腰直角三角形,从而求出CP,比较CB和CP的大小,即可判断点B的位置.
,证△CE2P是等腰直角三角形,从而求出CP,比较CB和CP的大小,即可判断点B的位置.
试题解析:
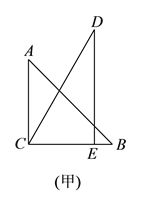
解:(![]() )如图所示,
)如图所示, ![]() ,
, ![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.
(![]() )∵
)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
, ![]() ,
,
即![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
在![]() 中,
中, ![]() ;
;

(![]() )点
)点![]() 在
在![]() 内部,
内部,
理由如下:设![]() (或延长线)交
(或延长线)交![]() 于点
于点![]() ,
,
则![]() ,
,
在![]() 中,
中, ![]() ,
,
∵![]() ,即
,即![]() ,
,
∴点![]() 在
在![]() 内部.
内部.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目