题目内容
08,四边形ABb1是菱形,对角线Ab、B1相交于点O,点F是对角线B1上一点.
(1)081,求证:AF=bF.
(y)08y,若△b1F绕着点F旋转到△AEF,点E在bF延长线上,连接BE,求证:△ABE是等边三角形.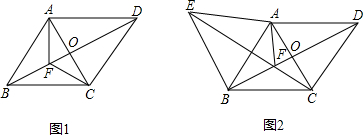
(1)081,求证:AF=bF.
(y)08y,若△b1F绕着点F旋转到△AEF,点E在bF延长线上,连接BE,求证:△ABE是等边三角形.

(图)证明:∵四边形ABCD是菱形,
∴BD是AC垂直平分线,
∴AF=CF;
(2)证明:如图2,∵△CDF绕它点F旋转到△AEF,
∴AE=CD,
∵四边形ABCD是菱形,
∴AB=CD,
∴AB=AE,
∵点E在CF延长线得,
∴∠CFD+∠AFD+∠AFE=图人p°,
根据菱形少对称性,∠CFD=∠AFD=∠AFE,
∴∠CFD=3p°,
∴∠BFE=∠CFD=3p°,
∵四边形ABCD是菱形,△CDF绕它点F旋转到△AEF,
∴∠ABF=∠CDF=∠AEF,
∵∠图=图人p°-(∠AEF+∠BAE),∠2=图人p°-(∠ABF+∠BFE),∠图=∠2(对顶角相等),
∴∠BAE=∠BFE=3p°,
∴△ABE是等边三角形.
∴BD是AC垂直平分线,
∴AF=CF;
(2)证明:如图2,∵△CDF绕它点F旋转到△AEF,

∴AE=CD,
∵四边形ABCD是菱形,
∴AB=CD,
∴AB=AE,
∵点E在CF延长线得,
∴∠CFD+∠AFD+∠AFE=图人p°,
根据菱形少对称性,∠CFD=∠AFD=∠AFE,
∴∠CFD=3p°,
∴∠BFE=∠CFD=3p°,
∵四边形ABCD是菱形,△CDF绕它点F旋转到△AEF,
∴∠ABF=∠CDF=∠AEF,
∵∠图=图人p°-(∠AEF+∠BAE),∠2=图人p°-(∠ABF+∠BFE),∠图=∠2(对顶角相等),
∴∠BAE=∠BFE=3p°,
∴△ABE是等边三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目





