题目内容
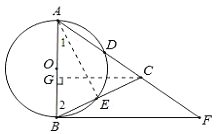
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠CBF=![]() ∠CAB.
∠CAB.
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF=![]() ,求BC和BF的长.
,求BC和BF的长.

【答案】(1)证明见解析;(2)BC=![]() ;
;![]() .
.
【解析】(1)连接AE,利用直径所对的圆周角是直角,从而判定直角三角形,利用直角三角形两锐角相等得到直角,从而证明∠ABF=90°.
(2)利用已知条件证得△AGC∽△ABF,利用比例式求得线段的长即可.
(1)证明:连接AE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠1+∠2=90°.
∵AB=AC,
∴∠1=![]() ∠CAB.
∠CAB.
∵∠CBF=![]() ∠CAB,
∠CAB,
∴∠1=∠CBF
∴∠CBF+∠2=90°
即∠ABF=90°
∵AB是⊙O的直径,
∴直线BF是⊙O的切线.
(2)解:过点C作CG⊥AB于G.
∵sin∠CBF=![]() ,∠1=∠CBF,
,∠1=∠CBF,
∴sin∠1=![]() ,
,
∵在Rt△AEB中,∠AEB=90°,AB=5,
∴BE=ABsin∠1=![]() ,
,
∵AB=AC,∠AEB=90°,
∴BC=2BE=2![]() ,
,
在Rt△ABE中,由勾股定理得AE=![]() =2
=2![]() ,
,
∴sin∠2=![]() =
=![]() =
=![]() ,cos∠2=
,cos∠2=![]() =
=![]() =
=![]() ,
,
在Rt△CBG中,可求得GC=4,GB=2,
∴AG=3,
∵GC∥BF,
∴△AGC∽△ABF,
∴![]() =
=![]() .
.
∴BF=![]() =
=![]() .
.

【题目】某同学上学期的数学历次测验成绩如下表所示:
测验类别 | 平时测验 | 期中测验 | 期末测验 | ||
第1次 | 第2次 | 第3次 | |||
成绩 | 100 | 106 | 106 | 105 | 110 |
(1)该同学上学期5次测验成绩的众数为 ,中位数为 ;
(2)该同学上学期数学平时成绩的平均数为 ;
(3)该同学上学期的总成绩是将平时测验的平均成绩、期中测验成绩、期末测验成绩按照2:3:5的比例计算所得,求该同学上学期数学学科的总评成绩(结果保留整数)。