Question

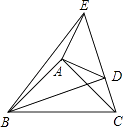
【题目】在直线上顺次取A，B，C三点，分别以AB，BC为边长在直线的同侧作正三角形，作得两个正三角形的另一顶点分别为D，E．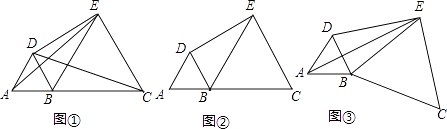

（1）如图①，连结CD，AE，求证：CD=AE；
（2）如图②，若AB=1，BC=2，求DE的长；
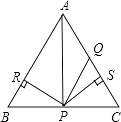
（3）如图③，将图②中的正三角形BEC绕B点作适当的旋转，连结AE，若有DE2+BE2=AE2 ， 试求∠DEB的度数．

Answer 1

【答案】
（1）证明：如图①中，∵△ABD和△ECB都是等边三角形，

∴AD=AB=BD，BC=BE=EC，∠ABD=∠EBC=60°，

∴∠ABE=∠DBC，

在△ABE和△DBC中，

，

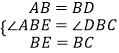∴△ABE≌△DBC，

∴AE=DC．

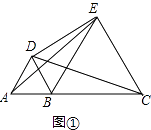
（2）解：如图②中，取BE中点F，连接DF．

∵BD=AB=1，BE=BC=2，∠ABD=∠EBC=60°，

∴BF=EF=1=BD，∠DBF=60°，

∴△DBF是等边三角形，

∴DF=BF=EF，∠DFB=60°，

∵∠BFD=∠FED+∠FDE，

∴∠FDE=∠FED=30°

∴∠EDB=180°﹣DEB∠DBE﹣∠DEB=90°，

∴DE= = = ．

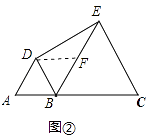
（3）解：如图③中，连接DC，

∵△ABD和△ECB都是等边三角形，

∴AD=AB=BD，BC=BE=EC，∠ABD=∠EBC=60°，

∴∠ABE=∠DBC，

在△ABE和△DBC中，

，

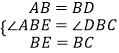∴△ABE≌△DBC，

∴AE=DC．

∵DE2+BE2=AE2，BE=CE，

∴DE2+CE2=CD2，

∴∠DEC=90°，

∵∠BEC=60°，

∴∠DEB=∠DEC﹣∠BEC=30°．

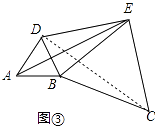
【解析】（1）欲证明CD=AE，只要证明△ABE≌△DBC即可．（2）如图②中，取BE中点F，连接DF，首先证明△BDE是直角三角形，再利用勾股定理即可．（3）如图③中，连接DC，先利用勾股定理的逆定理证明△DEC是直角三角形，得∠DEC=90°即可解决问题．
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识，掌握等边三角形的三个角都相等并且每个角都是60°，以及对勾股定理的概念的理解，了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．