Question

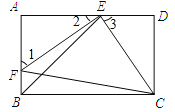
【题目】如图，AB是⊙O的直径，且点C为⊙O上的一点，∠BAC=30°，M是OA上一点，过M作AB的垂线交AC于点N，交BC的延长线于点E，直线CF交EN于点F，且∠ECF=∠E．

（1）证明：CF是⊙O的切线；

（2）设⊙O的半径为1，且AC=CE，求MO的长．

Answer 1

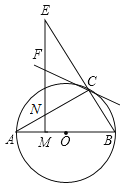
【答案】（1）答案见解析；（2）．

【解析】

（1）要证CF为⊙O的切线，只要证明∠OCF=90°即可；

（2）根据三角函数求得AC的长，从而可求得BE的长，再利用三角函数可求出MB的值，从而可得到MO的长．

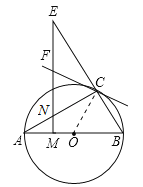
（1）如图，连接OC．

∵AB是⊙O的直径，∴∠ACB=90°．

∵∠BAC=30°，∴∠ABC=60°；

在Rt△EMB中，∵∠E+∠MBE=90°，∴∠E=30°；

∵∠E=∠ECF，∴∠ECF=30°，∴∠ECF+∠OCB=90°；

∵∠ECF+∠OCB+∠OCF=180°，∴∠OCF=90°，∴CF为⊙O的切线；

（2）在Rt△ACB中，∠A=30°，∠ACB=90°，

∴AC=ABcos30°=，BC=ABsin30°=1；

∵AC=CE，∴BE=BC+CE=1+．

在Rt△EMB中，∠E=30°，∠BME=90°，

∴MB=BEsin30°=，

∴MO=MB﹣OB=．