题目内容
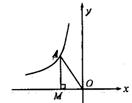
如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数 (x>0,k≠0)的图像经过线段BC的中点D.
(x>0,k≠0)的图像经过线段BC的中点D.
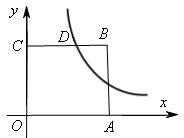
(1)求k的值;
(2)若点P(x,y)在该反比例函数的图像上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围。
 (x>0,k≠0)的图像经过线段BC的中点D.
(x>0,k≠0)的图像经过线段BC的中点D.
(1)求k的值;
(2)若点P(x,y)在该反比例函数的图像上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围。
(1)k=2(2)0<x<1或x>1
解:(1)∵正方形OABC中,点B的坐标为(2,2),点D是线段BC的中点,∴点B的坐标为(1,2)。
∵反比例函数 的图像经过点D,∴
的图像经过点D,∴ ,即k=2。
,即k=2。
(2)由(1)知反比例函数为 (x>0),
(x>0),
∵点P(x,y)在 (x>0)的图像上,
(x>0)的图像上,
∴设P(x,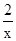 ),则R(0,
),则R(0,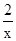 )。
)。
当0<x<1时,如图1,

∵四边形CQPR为矩形,∴Q(x,2)。
∴PR=x,PQ=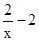 。
。
∴四边形CQPR的面积为: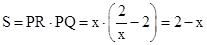 。
。
当x>1时,如图2,

∵四边形CQPR为矩形,∴Q(x,2)。
∴PR=x,PQ= 。
。
∴四边形CQPR的面积为: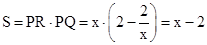 。
。
综上所述:S关于x的解析式为 , x的取值范围:0<x<1或x>1。
, x的取值范围:0<x<1或x>1。
(1)由点B的坐标可知BCC的长度,由点D 是BC的中点可得点D的坐标。由点D在反比例函数图象上,将点D的坐标代入可求得k的值。
(2)由题意可知,四边形CQPR是矩形,分0<x<1和x>1两种情况分别用x表示PQ,PR的长度,用矩形面积公式求解。
∵反比例函数
 的图像经过点D,∴
的图像经过点D,∴ ,即k=2。
,即k=2。(2)由(1)知反比例函数为
 (x>0),
(x>0),∵点P(x,y)在
 (x>0)的图像上,
(x>0)的图像上,∴设P(x,
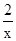 ),则R(0,
),则R(0,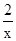 )。
)。当0<x<1时,如图1,

∵四边形CQPR为矩形,∴Q(x,2)。
∴PR=x,PQ=
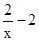 。
。∴四边形CQPR的面积为:
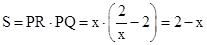 。
。当x>1时,如图2,

∵四边形CQPR为矩形,∴Q(x,2)。
∴PR=x,PQ=
 。
。∴四边形CQPR的面积为:
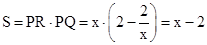 。
。综上所述:S关于x的解析式为
 , x的取值范围:0<x<1或x>1。
, x的取值范围:0<x<1或x>1。(1)由点B的坐标可知BCC的长度,由点D 是BC的中点可得点D的坐标。由点D在反比例函数图象上,将点D的坐标代入可求得k的值。
(2)由题意可知,四边形CQPR是矩形,分0<x<1和x>1两种情况分别用x表示PQ,PR的长度,用矩形面积公式求解。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
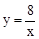 的图象经过点(﹣2,m),则m的值是
的图象经过点(﹣2,m),则m的值是
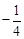
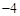
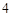
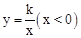 的图象经过点C,则k的值为 .
的图象经过点C,则k的值为 .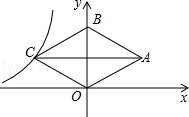
 在反比例函数
在反比例函数 的图象上,
的图象上,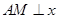 轴于点
轴于点 ,
, 的面积为3,则
的面积为3,则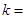 .
.
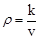 (k为常数,k≠0)其图象如图所示,则k的值为
(k为常数,k≠0)其图象如图所示,则k的值为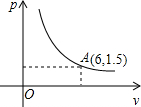
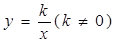 的图象经过点(
的图象经过点(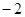 ,3),则它还经过点…( )
,3),则它还经过点…( )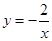 ,下列结论不正确的是
,下列结论不正确的是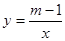 的图象在第一、三象限,则
的图象在第一、三象限,则 的取值范围是 ;在每一象限内y随x的增大而 。
的取值范围是 ;在每一象限内y随x的增大而 。