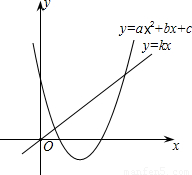题目内容
 一次函数y=kx与二次函数y=ax2+bx+c的图象如图所示,下列结论:
一次函数y=kx与二次函数y=ax2+bx+c的图象如图所示,下列结论:
①k>0;②a>0;③b>0;④c>0中,错误的结论序号是________.
③
分析:根据二次函数图象的开口方向来确定a的符号、由二次函数与y轴的交点来判断c的符号、由二次函数的对称轴的位置及a的符号确定b的符号;根据一次函数所经过的象限来确定k的符号.
解答:①∵一次函数y=kx经过第一、三象限,∴k>0;故本选项正确;
②∵二次函数y=ax2+bx+c的图象的开口向上,∴a>0;故本选项正确;
③根据图示知,二次函数y=ax2+bx+c的对称轴x=- >0,a>0(由①知),
>0,a>0(由①知),
∴b<0;故本选项错误;
④∵二次函数y=ax2+bx+c的图象与y轴交于正半轴,∴c>0;故本选项正确;
综上所述,错误的结论是③;
故答案是:③.
点评:此题主要考查二次函数图象与系数之间的关系,会利用对称轴的范围求2a与b的关系.此题将二次函数与一次函数综合在一起进行考查,增加了题目的研究性,也是中考中的热点题型.
分析:根据二次函数图象的开口方向来确定a的符号、由二次函数与y轴的交点来判断c的符号、由二次函数的对称轴的位置及a的符号确定b的符号;根据一次函数所经过的象限来确定k的符号.
解答:①∵一次函数y=kx经过第一、三象限,∴k>0;故本选项正确;
②∵二次函数y=ax2+bx+c的图象的开口向上,∴a>0;故本选项正确;
③根据图示知,二次函数y=ax2+bx+c的对称轴x=-
 >0,a>0(由①知),
>0,a>0(由①知),∴b<0;故本选项错误;
④∵二次函数y=ax2+bx+c的图象与y轴交于正半轴,∴c>0;故本选项正确;
综上所述,错误的结论是③;
故答案是:③.
点评:此题主要考查二次函数图象与系数之间的关系,会利用对称轴的范围求2a与b的关系.此题将二次函数与一次函数综合在一起进行考查,增加了题目的研究性,也是中考中的热点题型.

练习册系列答案
相关题目
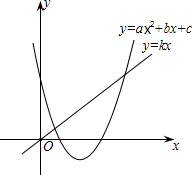 一次函数y=kx与二次函数y=ax2+bx+c的图象如图所示,下列结论:
一次函数y=kx与二次函数y=ax2+bx+c的图象如图所示,下列结论: