题目内容
（2009•晋江市质检）已知：如图，双曲线
经过点Q（2，n）．（1）求点Q的坐标；
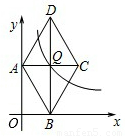
（2）若把菱形ABCD置于直角坐标系中，对角线AC与BD相交于点Q，且AC、BD分别与x轴、y轴平行，试求菱形ABCD的周长．
【答案】分析：（1）将Q点坐标代入双曲线中即可求出Q点的坐标；
（2）根据菱形的性质：对角线互相垂直平分以及Q点的坐标，即可求出A、B、C、D四点的坐标，根据A、B的坐标求出AB的长即可得出菱形的周长（求任意一边均可）．
解答：
解：（1）依题意得：n=3
∴点Q的坐标为（2，3）；
（2）∵四边形ABCD是菱形，
∴AC⊥BD，
∴∠AQB=90°，
在Rt△AQB中，AQ=2，BQ=3，
由勾股定理得：AB=
=
，
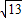∴菱形ABCD的周长为：4AB=4
．
点评：本题把反比例函数和菱形结合起来，综合利用它们的知识解决问题，同时也利用勾股定理等知识．
（2）根据菱形的性质：对角线互相垂直平分以及Q点的坐标，即可求出A、B、C、D四点的坐标，根据A、B的坐标求出AB的长即可得出菱形的周长（求任意一边均可）．
解答：
解：（1）依题意得：n=3∴点Q的坐标为（2，3）；
（2）∵四边形ABCD是菱形，
∴AC⊥BD，
∴∠AQB=90°，
在Rt△AQB中，AQ=2，BQ=3，
由勾股定理得：AB=
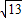=，∴菱形ABCD的周长为：4AB=4
．点评：本题把反比例函数和菱形结合起来，综合利用它们的知识解决问题，同时也利用勾股定理等知识．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
